ggplot2覚書⑨ 回帰線
引き続き「Rグラフィッククックブック」。

Rグラフィックスクックブック ―ggplot2によるグラフ作成のレシピ集
- 作者:Winston Chang
- 発売日: 2013/11/30
- メディア: 大型本
今回がとりあえずラスト。
過去分
ggplot2覚書③ 注釈(解釈補助) - まずは蝋の翼から。
ggplot2覚書⑤ 体裁(theme、テキストgeom)に関しての大枠 - まずは蝋の翼から。
ggplot2覚書⑥ theme詳細 凡例の設定 - まずは蝋の翼から。
ggplot2覚書⑦ theme詳細 facet - まずは蝋の翼から。
ggplot2覚書⑧ theme詳細 color - まずは蝋の翼から。
回帰線を引く
geom_smoothで引ける。methodで線のタイプを指定できる。"lm", "glm", "gam", "loess", 任意の関数が指定できる。デフォルトはloess
loess:平滑化線
"lowess" および "loess" という名前は "locally weighted scatter plot smooth (局所的に重み付けされた散布図平滑化)" から来ており、どちらの手法も局所的に重み付けされた線形回帰を使用してデータを平滑化します。 平滑化プロセスは、移動平均法のように、所定の範囲内で定義された隣接データ点によって平滑化した値が決まるため、局所的であると見なされます。所定の範囲に含まれるデータ点に対して回帰重み関数が定義されるため、このプロセスは重み付けを伴います。回帰重み関数に加え、ロバスト重み関数を使用して外れ値に対する耐性をこのプロセスにもたせることができます。さらに、この手法は回帰に使用するモデルによって区別されます。lowess は線形多項式を使用し、loess は 2 次多項式を使用します。
とのこと。
データのフィルター処理と平滑化 - MATLAB & Simulink - MathWorks 日本
厳密に範囲を決める場合は、はクロスバリデーションをして決めるらしい。
ESI友の会:メタボロミクス若手会 - 2. LOWESSとSplineの理論
範囲が3だとすると、(n-1, n, n+1)番目が範囲となり、nを中心としてnを重み強め、nからxが離れるほど重みを軽くした重み付け回帰線を引く。これを、(n-1, n, n+1)、(n, n+1, n+2)、(n+1, n+2, n+3)、(n+2, n+3, n+4)...番目それぞれに対しておこない引かれた線をなめらかに繋げて1つの非線形曲線にするイメージか?
範囲はspan(デフォルト0.75)で指示する。この数字自体はなにを表しているか不明。その%範囲を指示する場合が多いようだが。。。
また、範囲内に引いていく回帰線はdegreeで何次式での回帰線を引くか指示ができる(デフォルトは二次関数)。
なお、aes内でweightを指示することで範囲内の位置による重み付け以外にそもそもの回帰式自体にも重み付けができる。
どういう意味があるかというと、最小二乗回帰線(OLS)でいうところ、加重最小二乗法(WLS)のような感じにできる。WLSは不均一分散データに対して、分散の逆数を重みとして変換することで均一分散にしてOLSする手法。何故不均一分散がいけないかは過去記事参照。
#デフォルト g0 <- mtcars %>% ggplot(aes(mpg, disp)) + geom_point() + geom_smooth() #デフォルトを明示 g1 <- mtcars %>% ggplot(aes(mpg, disp)) + geom_point() + geom_smooth(method = "loess",method.args= list(degree = 2), span = 0.75 ) #span変更 g2 <- mtcars %>% ggplot(aes(mpg, disp)) + geom_point() + geom_smooth((method = "loess",method.args= list(degree = 2), span = 0.2) #degree変更 g3 <- mtcars %>% ggplot(aes(mpg, disp)) + geom_point() + geom_smooth((method = "loess",method.args= list(degree = 1), span = 0.75) (g0 | g1) / (g2|g3)
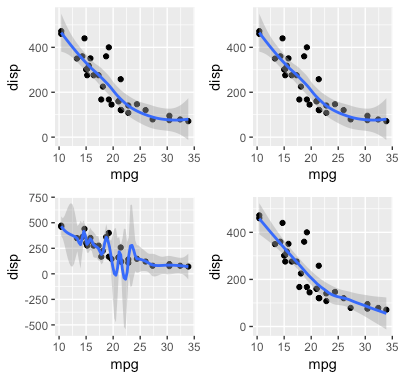
glm:一般化線形モデル
glm(一般化線形モデル)では、familyを指定すると一般化線形モデル内の様々なモデルが使用できる。GLMのパラメータなどの詳細は過去記事参照。基本的に指定の仕方はglm関数とほぼ同じ。
library(MASS) # データセットの読み込み b <- biopsy b$classn[b$class=="benign"] <- 0 b$classn[b$class=="malignant"] <- 1 # ロジスティクス回帰 ggplot(b, aes(x=V1, y=classn)) + geom_point(position=position_jitter(width=0.3, height=0.06), alpha=0.4, shape=21, size=1.5) + # method.argsにlistでfamilyとして確率分布とlink関数を指定する geom_smooth(method = "glm", method.args = list(family = binomial(link = "logit")))
