3章傾向スコア

傾向スコアは過去記事で何回か扱った。

knknkn.hatenablog.com

CIA(Conditional Independence Assumption)では、共変量の値が同一のユーザー同士下ではRCTになる仮定に対し、傾向スコアでは傾向スコアが同じユーザーの中ではRCTになる仮定をしている。前者は共変量Xの数が多かったり取る値が大きいことから難しかったが、傾向スコアは0.0~1.0の1つの値さえ一致していれば良いから楽。
共変量Xを1次元かつ0.0~1.0の値に射影したのが傾向スコアと考えることができる。

$CIA：{Y_0, Y_1} ⊥ Z_i | X_i$
$傾向スコア：{Y_0, Y_1} ⊥ Z | P(X)$

IPW

介入Zの割り振りは傾向スコアP(X)に従っている。そのため、例えばP(X)=0.7の場合は70%がZ=1、30%はZ=0として観測されている。つまり。Z=1ではP(X)が高いサンプルに偏ったサンプリングになりその平均と真の平均とのズレがセレクションバイアスとして現れる。

このことを考慮して、傾向スコアの逆数を重みとした重み付き平均を取る。つまり、よく観測される(傾向スコアが高い)値の重みを低くし、逆にあまり観測されない値の重みを大きくする。

イメージでいえば、割り振りは傾向スコアに依存しているので傾向スコアが低いデータはサンプル数がRCTと比べて少なくなる。そのため、傾向スコアが低いサンプル数をRCTと同等のサンプル数にするために重み付けによって擬似的にサンプルのかさ増しをおこなうことでRCTと同様のサンプル分布にし、平均を真の平均に近づけている。著作権の関係で載せないが、図3.4の模式図がわかりやすい。

このとき、割り振りZに関わらない介入があった場合のY、 $Y^{(1)} = \sum_{i=1}^{N} \frac{Z_i Y_i}{P(X_i)} / \sum_{i=1}^{N} \frac{Z_i}{P(X_i)}$ となる。介入がなかった場合の $Y^{(1)}$ はPではなく1-Pを用いる。
ここから、 $ATE = E(Y^{(1)}) = E(Y^{(0)})$ を求めることができる。

# (8) 逆確率重み付き推定（IPW）
## ライブラリの読み込み
library("WeightIt")

## 重みの推定
weighting <- weightit(treatment ~ recency + history + channel,
              data = biased_data,
              method = "ps",
              estimand = "ATE")

## 重み付きデータでの効果の推定
IPW_result <- lm(data = biased_data,
                 formula = spend ~ treatment,
                 weights = weighting$weights) %>%
  tidy()

# term        estimate std.error statistic     p.value
# <chr>          <dbl>     <dbl>     <dbl>       <dbl>
# 1 (Intercept)    0.580     0.116      4.99 0.000000601
# 2 treatment      0.870     0.165      5.27 0.000000136

github.com

https://cran.r-project.org/web/packages/WeightIt/WeightIt.pdf

傾向スコアの注意点

共変量のバランス

傾向スコアにおいて、共変量のバランスが取れているかが重要となる。
つまり、共変量の各変数において、介入群と非介入群での平均差(横軸)がどれくらいなのかを調べることで、介入群と非介入群で違いがないか(0に近いか）が重要となる。

このとき、差が大きいということは介入群と非介入群において分布が違うこととなり $傾向スコア：{Y_0, Y_1} ⊥ (Z | P(X))$ を満たしていないこととなる。

# (9) 共変量のバランスを確認
##ライブラリの読み込み
library("cobalt")

## 重み付きデータでの共変量のバランス
love.plot(weighting,
          threshold = .1)

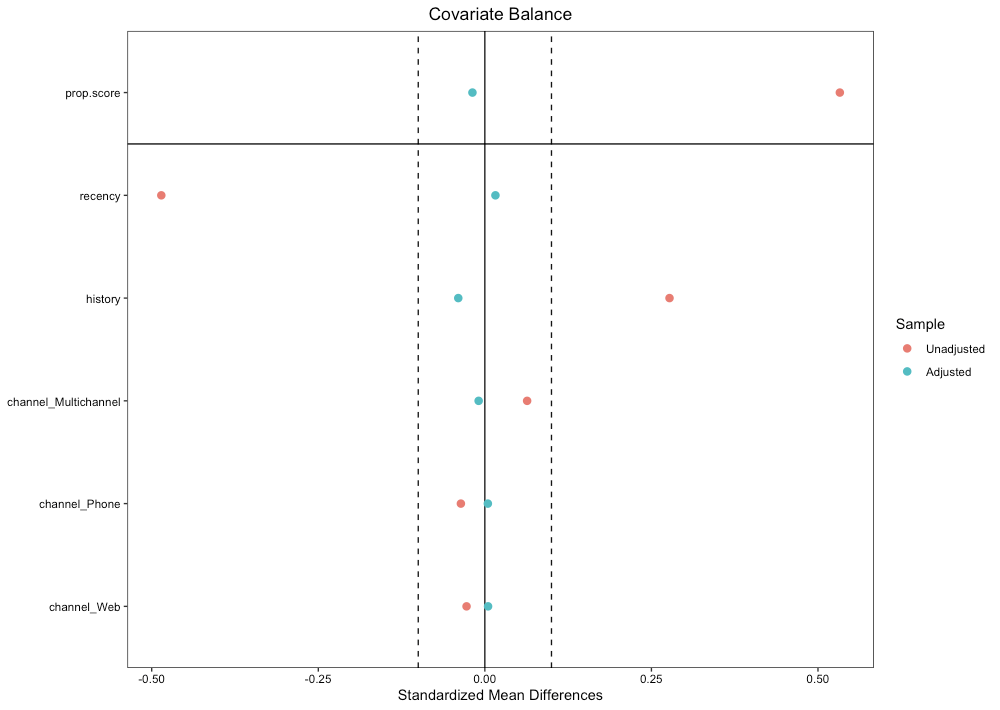
f:id:chito_ng:20200419222052p:plain

また、IPWでは逆確率重み付けという性質上、介入群と非介入群で共変量のバランスが悪い場合に傾向スコアが極端な値を取りやすい。そのとき、例えば0.01%の場合10000倍にかさ増しされるのでそのサンプルの誤差の影響が非常に大きくなり推定値が歪んでしまう。このようなときは上述の共変量のバランスが調整後も大きい値を取ることから検出することができる。また、一定以下の傾向スコアを取る値に対しては除外をするなどの対処も考えられる。

ただし、その場合は除外した分布が歪むため真の分布ではないのでは？という話もある（下記ブログの「コモンサポートについて」参照。

qiita.com