はじめに

昔、非線形モデルのプロビット・トービット・へーキッドについて記事を書いた。 knknkn.hatenablog.com

実際に中身の確認および、当時はなんとなく理解だったので改めて書き直す

非線形モデル

ある事象に対して、xxするか/xxしないかというダミー変数Yiに対して、xxする確率を求めたい場合に通常のOLS同様にモデルを $Y_i= α + βX_i+\epsilon_i$ とすると以下の問題が起きる。

$Y_i が (0,1)$ 以外の範囲を取る
誤差項が正規分布しない
誤差項の分散はXiとともに変化する（不均一分散）

2,3の理由から、OLS推定量は有効ではない。また、1.の理由から $Y_iが(0,1)$ を取るようなモデルに変える必要がある。 $X_iによって(0,1)$ を取る関数として累積密度関数を与え、非線形モデルを考えるとこの問題は解決する。
つまり、Φを累積分布関数として

$p_i = Pr(Y_i = 1 | X_i) = Φ( α + βX_i + \epsilon_i)$

となるモデルを仮定する。これは、Xiの一次式 $α + βX_i + \epsilon_i$ があり、この一次式が累積分布関数Φによって変換され $p_i$ となるといえる。

この考え方は潜在変数モデルという選択行動モデルが背景にある。
これは、効用を示す観測できないある変数（潜在変数） $Y^*_i$ があり、その効用の値に応じて目的の確率が変わると考えるモデルとなる。
潜在変数を $Y^*_i$ とすると、 $Y_i = 1$ のときの効用が $Y_i = 0$ の効用を上回るかどうかで $Y_i$ の値が決まるため

$Y^*_i = α + βX_i + \epsilon_i \leq 0$ ( $Y_i = 1$ の効用 $\leq Y_i = 0$ の効用) のとき　 $Y_i = 0$
tex:Y^*_i = α + βX_i + \epsilon_i > 0 のとき　 $Y_i = 1$

のように記述でき、この $Y^*_i$ 閾値を超えたとき目的変数 $Y_i$ が1を取る、と考える。

Y これは前述のモデルに置き換えると $Y_i = 1$ となる確率 $p_i$ は

$p_i = Pr(Y_i = 1 | X_i) = Pr(Y^*_i = α + βX_i + \epsilon_i > 0 | X_i) = Φ( Y^*_i = α + βX_i + ε_i)$

となっている。先程

Xiの一次式 $α + βX_i + \epsilon_i$ があり、この一次式が累積分布関数Φによって変換され $p_i$ となるといえる。

と記載したが、潜在変数を踏まえると

潜在変数 $Y^*_i$ の値に応じた累積分布関数Φによって $Y_i$ が1となる確率が求まる]

と書き直すことができる。

ここで累積密度関数Φとして、ロジット分布を用いる場合をロジットモデル、標準正規分布を用いる場合はプロビットモデルという。なお、このとき推定量として最尤推定量を用いる。

打ち切りデータと切断データ

世の中には、本来は0未満のデータとなっているのに0として観測される **打ち切りデータ** や、そもそも観測がおきない **切断データ** が存在する。

例えば、前者はサッカー選手の試合出場時間など。試合は能力(など）がある一定以上を満たさないと試合に出場できない。出場時間がマイナス、というのはありえないため出場時間は0として打ち切られて観測される。
後者の例として、高齢者の賃金など。賃金は能力(など）によって決まるが、そもそも働いている高齢者内でしか賃金が観測されない。つまり、想定したい母集団は高齢者全体だが、標本として抽出しているのは働いている高齢者だけになっている。

どのような問題が起きるか

実際にどのような問題が起きるかを、以下のような確率分布からの観測値を用いて考える。

変数 $(x, y)$ の真の関係が $y = 1 + x$ とする
挙動確認のために、この関係に対してランダムなノイズを加えた $y_i = 1 + x_i + \epsilon_i$ から1000個データを生成する。

library(tidyverse)
library(censReg)
library(modelr)

library(viridis)
library(RColorBrewer)
cols = brewer.pal(9, 'Set1')

set.seed(1)

N = 1000
x = rnorm(N)
e = rnorm(N)
a = 1
b = 1
y = a + b * x + e

ここで、前述のような問題を考えるための観測値を作成する。

打ち切りが発生した場合、y < 0 を0に変換したデータdf_cut
切断が発生した場合、y < 0 を削除したデータdf_trunc

# 通常
df = tibble(x = x, y = y) %>%
    mutate(type = 'Normal')

# 打ち切り
df_censored = df %>% 
    mutate(y = if_else(y < 0, 0, y), type = 'Censored')

# 切断
df_truncated = df %>% 
    filter(y >= 0) %>%
    mutate(type = 'Truncated') 

df_union = df %>% 
    bind_rows(df_censored, df_truncated) %>% 
    mutate(type = factor(type, levels = c('Normal', 'Censored', 'Truncated')))

それぞれ可視化をすると、Normalが打ち切られる前のデータ、Censoredが打ち切られたデータ、Truncatedが切断されたデータとなる。

df_union %>%
    ggplot(aes(x, y, color = type)) +
    geom_point(size = 3, alpha = 0.2) +
    facet_wrap(~type) +
    scale_color_brewer(palette='Set1')

f:id:chito_ng:20190127183903p:plain

これらに対してOLSをおこなう。
黒線で真の関係モデル $y = 1 + x$ 、色線でそれぞれの点から推定されるOLSとなる。

df_union %>%
    ggplot(aes(x, y, color = type)) +
    geom_point(size = 3, alpha = 0.2) +
    geom_abline(intercept = a, slope = b, color = "black", size=1) + 
    geom_smooth(method="glm", se=F, size=2) +
    facet_wrap(~type) +
    scale_color_brewer(palette='Set1')

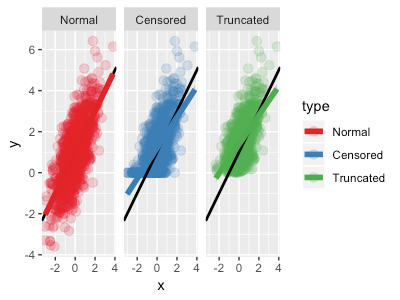
f:id:chito_ng:20190127183957p:plain

グラフの結果からわかるように、

打ち切り/切断が発生していないデータにOLSを適用すると、真の関係を完璧に捉えることができる。
打ち切りデータ(Cutted)にOLSを適用すると係数が過小に推定されてしまう（本当の関係よりも傾きが緩くなる）。これは、本当は0より小さい値をとっているデータが0に変換されていることが原因で xx のインパクトが過小評価されていることが原因。
切断データ(Truncated)にOLSを適用すると打ち切りデータと同様であるが、打ち切りデータ以上に過小評価されている。これは、本当は0より小さい値をとっている除去され、0位上のデータだけで推定がおこなわれていることが原因。

念のために、数値として確認したい場合は以下。

df %>% lm(y ~ x, data =.)

Call:
lm(formula = y ~ x, data = .)

Coefficients:
(Intercept)            x  
     0.9838       1.0064

df_censored %>% lm(y ~ x, data =.)

Call:
lm(formula = y ~ x, data = .)

Coefficients:
(Intercept)            x  
     1.2041       0.7489

df_truncated %>% lm(y ~ x, data =.)

Call:
lm(formula = y ~ x, data = .)

Coefficients:
(Intercept)            x  
     1.3832       0.7094

Tobitモデルとは

前述のように、OLSで打ち切り/切断データを用いる場合、打ち切り/切断されたことによるバイアスが起こり、推定量が過小評価される。このバイアスは、プロビットモデル/ロジットモデルで考えた潜在変数モデルを用いた、トービットモデルを用いることで克服できると知られている。

トービットモデルは潜在変数を $Y^*_i$ とすると以下のモデルで表せる。

$Y^*_i = α + βX_i + \epsilon_i > 0 で Yi = Y^*_i = α + βX_i + \epsilon_i$ ...(1)
$Y^*_i = α + βX_i + \epsilon_i \leq 0 で Y_i = 0$ ... (2)

つまり、潜在変数 $Y^*_i$ がある閾値(簡易化のため上記では0だが実際は0じゃなくても定数であればよい)を超えた場合は $Y_i$ はそのまま $Y^*_i$ として観測され、閾値に満たない場合は $Y_i = 0$ として観測される。

(1)は誤差項に正規分布を仮定しているので確率分布は
[tex:f(y_i | x_i) = 2\pi^{-\frac{1}{2}}(\sigma²)^{-\frac{1}{2}}e^\frac{-(y_i - α - βx_i)²}{2\sigma²}] となる。

(2)は
$f(y_i = 0 |x_i) = 1 - Φ( \frac{α+βx_i}{σ})$ となる。

トービットモデルではこれらをYi= 0で0、Yi > 0で1になるダミー変数di = {0,1}で場合分けすることにより、以下の分布式で表せる。 [tex:f(y_i | x_i) = f(y_i | x_i)^{d_i} f(0 | x_i)^{1 - d_i}= [(2\pi)^{-\frac{1}{2}}(\sigma²)^{-\frac{1}{2}}e^\frac{-(y_i - α - βx_i)²}{2\sigma²}]^{d_i} [1 - Φ( \frac{α+βx_i}{σ} )]^{1 - d_i}]

この分布式に対して最尤推定することでパラメータを求めることができる。

ただし、トービットモデルは $ε_i$ が正規分布かつ不均一分散を仮定した最尤推定をしているので、真のモデルが仮定を満たさない場合は最尤推定量は一致性を持たないので注意。

プロビットモデルと比較して考えると、 - 潜在変数 $Y^*_i$ が閾値以上で $Y_i = 1$ 、閾値以下で $Y_i = 0$ になるように $Y^*_i$ を累積分布関数Φでマッピング (プロビットモデル) - 潜在変数 $Y^*_i$ が閾値以上で $Y_i = Y^*_i$ 、閾値以下で $Y_i = 0$ になるように $Y^*_i$ を場合分けした分布でマッピング (トービットモデル) といった違いがある。