この章はなにか

高次元のモデルを作成するときに、オーバーフィットを避けた良い予測をできるモデル選択(変数選択)において注意すべき点が色々とある。

この節はなにか

モデル選択の前に、そもそも予測性能を見るときは何を指標にしたらいいかという話。通常の $R^2$ (以下R2)ではなく、trainと別のデータに対するR2を見る必要がある。

Out-of-Sample Performance

前章で紹介したdeviance(逸脱度)はあるデータに対して作成したモデルがどれくらいフィットしているかを測る指標。

knknkn.hatenablog.com

モデル作成の意図が意思決定や予測のときは一般的なtrainingデータ(IS:In-Sample)に対するdevianceを気にする必要はないが、trainingとは別の新規データ(OOS:Out-Of-Sample)に対するdevianceを測る必要がある(逆に、IS devianceはモデル解釈のときに使用する？）。

このとき、同様にモデルの説明力を表す $R^2 = 1 - \frac{Residual Deviance}{Null Deviance}$ はOOSに対する R2を気にする必要がある。
データ $(x_1,y_1) , ...(x_n,y_n), (x_{n+1},y_{n+1}),...,(x_{n+m},y_{n+m})$ のうちnまでを用いて作成されたモデルの係数 $\hat{\beta}$ とすると、ISとOOSでのR2に用いるdevianceは以下となる。

ISのR2では、 $dev_{IS}(\hat{\beta}) = \sum_{i=0}^n (y_i - x_i' \hat{\beta})^2$
OOSのR2では、 $dev_{OOS}(\hat{\beta}) = \sum_{i=n+1}^{n+m} (y_i - x_i' \hat{\beta})^2$

何故予測の際にISではなくOOSで見るかというと、ISを用いたモデルは「ISでたまたま発生しているノイズや偏り」なども含めて構築される。そのため、IS-R2でモデルの予測性能を評価すると、一般性を失ったオーバーフィット状態での評価をおこなうことになる。一方で、OOS-R2で評価をすると、trainとは別のデータで評価するので「ISでたまたま発生しているノイズや偏り」は評価に対してマイナスになり一般性を持った評価となる。

実データ分析

n=1500, 200次元の半導体データに対して、chipが正しいか間違っているかのバイナリ予測モデルを用いる。

github.com

library(tidyverse)
SC <- read.csv("semiconductor.csv")

## full model
full <- glm(FAIL ~ ., data=SC, family=binomial)
# Degrees of Freedom: 1476 Total (i.e. Null);  1276 Residual
# Null Deviance:       731.6 
# Residual Deviance: 320.3     AIC: 722.3

# R^2
1 - full$deviance/full$null.deviance # 1 - Residual Deviance/Null Deviance
# => 0.5621432

全200次元を用いたIS-R2は0.56となった。

検定

200次元の検定結果は以下となる。

## grab p-values
pvals <- summary(full)$coef[-1,4] #-1 to drop the intercept

## plot them: it looks like we have some signal here
hist(pvals, xlab="p-value", main="", col="lightblue")

f:id:chito_ng:20200320135204p:plain

1章のFDRあたりの議論で、「p値が一様分布から独立に生成されている」と仮定されるが今回は0付近にスパイクがある。

knknkn.hatenablog.com

つまり、この仮定を満たさないなにかしらの理由があると考えられる。
Benjamini-Hochberg(BH)法を用いてFDRをおこなう*1 。

## At 10% FDR, we get 25 `signif'
fdr_cut <- function(pvals, q=0.1){
  pvals <- sort(pvals[!is.na(pvals)])
  N <- length(pvals)
  k <- rank(pvals, ties.method="min")
  alpha <- max(pvals[ pvals<= (q*k/(N+1)) ])
  
  plot(pvals, log="xy", xlab="order", main=sprintf("FDR of %g",q),
       ylab="p-value", bty="n", col=c(8,2)[(pvals<=alpha) + 1], pch=20)
  lines(1:N, q*(1:N)/(N+1))
  
  return(alpha)
}

fdr_cut(pvals)

このとき、カットオフ基準下にある有意とされる25個ほどの変数を用いてdevianceを再度計算する。

## Re-run a cut regression using only these 25
( signif <- which(pvals <= 0.0122) )
# SIG2  SIG17  SIG19  SIG20  SIG22  SIG24  SIG46  SIG47  SIG49  SIG50  SIG52  SIG59  SIG61 
# 2     17     19     20     22     24     46     47     49     50     52     59     61 
# SIG69  SIG83 SIG102 SIG111 SIG136 SIG142 SIG154 SIG166 SIG178 SIG186 SIG189 SIG200 
# 69     83    102    111    136    142    154    166    178    186    189    200 

cut <- glm(FAIL ~ ., data=SC[,c("FAIL", names(signif))], family="binomial")
1 - cut$deviance/cut$null.deviance # new in-sample R2
# 0.1811822

結果として、このcut-offモデルのIS-R2は0.18となった。これは、先程のfull modelでのIS-R2の0.56と比べて非常に小さな値となる。これは、IS-R2の特徴として、(有意でないもの含めて）変数を増やせば増やすほどIS-R2は増加することが理由となる。

K-Fold Out-Of-Sample Validation

予測性能を評価するOOS-R2を用いる場合、training(IS)に入れていない未知のデータを用いるためK-Fold Out-Of-Sample Validationをおこなう。これは、機械学習で用いるK-Fold Cross Validationと同じもの。全データからいくつかデータを除いてtrainをし、除いたデータで評価をK回繰り返す。

これを用いて先程のfull modelと、先程のcut-offモデルでのOOS-R2を見ることで各モデルの予測性能を比較してみる。

まず、OOS-R2を計算する関数を作成。

## Out of sample prediction experiment
## first, define the deviance and R2 functions

## pred must be probabilities (0<pred<1) for binomial
deviance <- function(y, pred, family=c("gaussian","binomial")){
  family <- match.arg(family)
  if(family=="gaussian"){
    return( sum( (y-pred)^2 ) )
  }else{
    if(is.factor(y)) y <- as.numeric(y)>1
    return( -2*sum( y*log(pred) + (1-y)*log(1-pred) ) )
  }
}

## get null deviance too, and return R2
R2 <- function(y, pred, family=c("gaussian","binomial")){
  fam <- match.arg(family)
  if(fam=="binomial"){
    if(is.factor(y)){ y <- as.numeric(y)>1 }
  }
  dev <- deviance(y, pred, family=fam)
  dev0 <- deviance(y, mean(y), family=fam)
  return(1-dev/dev0)
}

そして、K-Fold Out-Of-Sample Validationをおこなう。なお、gitコードにcutvar オブジェクトが無かったので cutvar = c("FAIL", names(signif)) をコードに追加している。

cutvar = c("FAIL", names(signif)) # 無かったので追加
for(k in 1:K){ 
  train <- which(foldid!=k) # train on all but fold `k'
  
  ## fit the two regressions
  rfull <- glm(FAIL~., data=SC, subset=train, family=binomial)
  rcut <- glm(FAIL~., data=SC[,cutvar], subset=train, family=binomial)
  
  ## get predictions: type=response so we have probabilities
  predfull <- predict(rfull, newdata=SC[-train,], type="response")
  predcut <- predict(rcut, newdata=SC[-train,], type="response")
  
  ## calculate and log R2
  OOS$full[k] <- R2(y=SC$FAIL[-train], pred=predfull, family="binomial")
  OOS$cut[k] <- R2(y=SC$FAIL[-train], pred=predcut, family="binomial")
  
  ## print progress
  cat(k, " ")
}
## plot it in plum
par(mai=c(.9,.9,.1,.1))
boxplot(OOS, col="plum", ylab="R2", xlab="model", bty="n")

## what are the average OOS R2?
colMeans(OOS) # WOW!  Full model really sucks.
# full         cut 
# -7.40218852  0.06442222

f:id:chito_ng:20200320143107p:plain

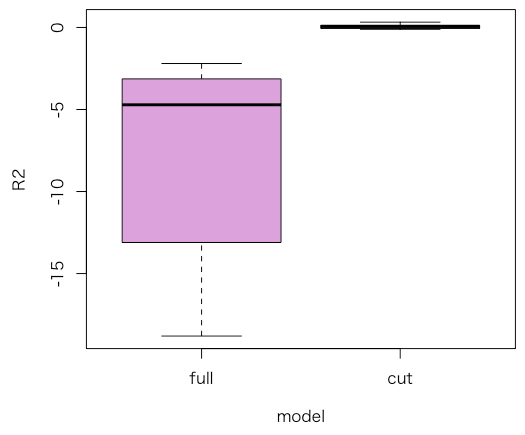
結果として、fullモデルよりcut-offモデルの方がOOS-R2、つまり予測性能は高い。
また、fullモデルはマイナスになっているがこれは、 $R^2 = 1 - \frac{Residual deviance}{Null deviance}$ より、Residual deviance > Null deviance(期待値だけのモデル) となっていることが理由となっている。