2021年の振り返りと2022年に何をしていくか
仕事とプライベートどちらも大きな変革がありました。そのため2022年は色々やろうと思ったのでそれぞれ書いていこうと思います。端的に書くと、しくじり体験記です。
シニアDSになったけれども・・・
2020年末くらいにシニアDSに昇格したので1年で色々とやったけれど シニアとしてうまくできてなかったなーという話。
マネジやろうと思ったけどうまくできなかったよ
弊社のシニアDSというポジションはそのままマネジメント方向に進んでもいいし、DSっぷりを上げてもいいという分岐点的な立ち位置。その中で、私はマネジメント方向を希望したため、次のキャリア「マネージャー」としての能力を上げていこうということでチーム運営や採用などのマネージャーの仕事を現マネージャーと一緒にやることになった。 それから1年、結論としてはまったくうまくやることができなかった。
私はマネージャーではなくマネージャー予備軍なのでマネジメント業務を副業務としてやりつつ主業務の案件もやらないといけない。あくまでメインは案件。そのため、主業務をメインでやりつつ副業務をする時間を確保して回す必要があったが、うまくやることができず、主業務の案件に圧迫され副業務のマネジメント業務は中途半端にしかやることができなかった。
つまりは、今まで通りのやり方で主業務をやっていたので副業務まではできなかったという話。
このような二足のわらじが無理だった原因を振り返って考えると、時間の使い方が大きい。
今までは基本的に1案件にのみリソースを割く仕事が多かったがマルチタスク(案件&マネジ)になるとうまく時間配分を考え、それに応じて1タスクに対してどこまでやるかの判断や追加タスクへのコントロールをしないといけなかった。
例えば「この部分を追加で深堀りしてくれないか?」という外部からの要望はただただ受けるのではなくちゃんと「深堀ることによるメリットに対してのトレードオフ」を考えてコミュニケーションを取るべきだった。
この問題は、マルチタスクだから起きたことではなくシングルタスクのときにも実はちゃんとやらないといけなかったがシングルタスクゆえに表面化しづらかった問題でもとから起きていた問題のように思う。
ビジネス力がごみだったよ
これは前から問題意識はあったけれど、「自分でビジネス課題を見つけてデータサイエンスに落とし込む」というところが色々試してみたけれどうまくいかなかった。
具体的には、Slackやビジネス系部署(営業やコンサル部署)の定例会議に出たりで社内情報をinputしてみたもののデータサイエンスに落とし込むアイデアが思い浮かばなかったし、そもそもビジネス課題も良い筋を発見できなかった。
また、案件としてやってくるタスクも、案件なのでなにかしらビジネス課題はあるものの、既存のソリューションとしての落とし込みしかできずより良いソリューションまで展開できなかった(もちろん既存で十分なものもあるので必ずしも新たなものを産まなくてもいいけれども)。
それらを踏まえて2022年はどうしたらよいか
結局のところ、二足のわらじを履く前に一足のわらじですらうまく履けていないことがわかった。
これはもはやシニアDSか?と思いつつ、少なくともマネージャー目指す以前にDSとしてちゃんとせーや、ということで2021年末に色々考えた結果、いったんマネージャー予備軍活動を停止して一足のわらじをちゃんと履けるようにして、それから改めてマネージャーを目指そうと思った。
ちゃんと立ち止まろう
タイムマネジメントにせよ、アイデアにせよ、新たなソリューションにせよ、共通した問題が原因のひとつとなっている。それは「ちゃんと立ち止まらないで脳死で動く」こと。
過去にワンオペDSをしていたときにタスクが大量にあって何か考えずにひたすら処理をしないと捌けないということが2年くらいあった(そもそも深夜までやってやっと終わらせれたので捌けてはない)。また、こちらでコントロールできない要因などでやらざるを得ない経験も多かった。そこから「とにかく来たものは受け入れてさっさと片付ける」という癖が染み付いてしまっている。 また、無能と思われるのが嫌だという自分の気質や自信の無さもあり、何も出ない期間を極力避けようとする、つまり「短期間でアウトプットを出そうとする」癖がある。
これらがまとまった(あるいは相互作用した)結果「熟考することなく反射だけでなにかしようとする」人間が生まれた。
「タイムマネジメント」は、どうやったら案件やタスクをコントロールできるか、タスクをマルチにこなせるか考えずに脳死で来たものを片付けようとするからうまくいかなかった。
「アイデアが出ない」は、表層的情報だけでは出てこないアイデアを表層的情報だけで得ようとしたのでうまくいかなかった。
「ビジネス課題」に対しては、課題やモデルについて深く考えずに手癖やぱっと思い浮かぶことだけで処理しようとするから何もでてこなかった。
他にも色々と原因はあるだろうが、「熟考することなく反射だけでなにかしようとする」ことをやめるといくらかは改善するように思える。
例えるなら、素振り回数さえ重ねたら強くなれると思ってひたすら数をこなすために脳死で素振りだけしているよりも、1本1本の素振りに対して考えて試行錯誤しながら素振りをする方が強くなれるにきまっている。
そのため、案件や追加タスクなど新たに発生したなにかに対して「何も出ない期間を恐れない」で「いったん立ち止まって考える」ことを2022年の目標として入れたい。
ちゃんと楽しもう
「ちゃんと立ち止まろう」に繋がる話ではあるが、案件にせよ情報にせよ左から右に流すことを急ぎすぎて、「ただの処理すべき対象」としてしか見ていないように感じた。素振りの例でいうならば素振りを「バッドを振る行為」ではなく「(数を増やすための)カウント対象の行為」としてしか見てないので何の情動も起こらない。
話はいったん逸れるが、上司(現マネージャー)が常に「あの案件どうやったら解決できるかな」「こういうモデルだとうまくいきそうだけどXXという問題が出てくるからいい解決策ないかな」みたいに考えつつ、良さげことを思いついたから実装して気づいたらソリューションができてたみたいなことがよくある。
なんでポンポンと色んなアイデアが思い浮かぶのかなと不思議だったが、「仕事(処理すべき対象)」としてこういうことをしているのではなく、「なんでこうなってるんだろう?」「こうやったらうまくいくかも」と、気になったことを試したりして楽しんでるだけなんですよね。仕事を前述のように「ただの処理すべき対象」として捉えている自分との明確な違いだと思う。
ビジネス課題に対して、クイズのように楽しんで考えたり、どうやったらより良い解答になるか考えたりするからこそ良いアイデアが出る。
しかし、これは真似ようと思っても「XXを好きになる/楽しむ」って本人の興味対象や気質に依るので真似るもクソもない。実際、前述のように「色々なMTGに出る」「slackや議事録を読む」のようなinput行動だけ真似たり、「あの案件どうやったら解決できるかな」「こういうモデルだとうまくいきそうだけどXXという問題が出てくるからいい解決策ないかな」と考える時間を設けたが結局は「楽しんでやってない」ので「なるほど」で終わって「これってこうするとよくなるのでは!?」みたいな情動はわかなかったからか、うまくいかなかったです。
ただ、「大して興味はなかったが知れば知るほど面白くなった」みたいなことは往々にしてあり、自分は仕事のドメイン知識に対して表層は知っているけど面白いと考えれるほど深いところまでは知らないだけな気がする。
更に言えば、いわゆる「当事者意識」が足りず部外者感覚なので興味が出るわけがない。
そのため、「興味を持って情報を受け取る」という心構えの改革が必要となる。
ところで「アイデアのつくり方」という古典名著があってその中に、「小説家になりたいならタクシー運転手を一日中観察しろ。この男がこの世界中の他のどの運転手ともちがった一人の人物になるまで、君はこの男を研究しなければいけない。」という話がある。これは要するに「タクシーを運転する人間」のような普遍的で特徴のない対象として見るのではなく、一人の人間としてみることで特殊性を捉えろ、解像度を上げろという話。(この本には書いてないが、)このような考え方で運転手をみると「なんでこの人はこのタイミングで減速をしたのだろう?」「なぜこの位置で流しをしていたのだろう?」と考えその人に興味がわき解像度が上がる。なんでもこの視点が大事に思う。
つまり、楽しむためにはそもそもその対象を興味を持って見ないといけないのだ。
また、前節の「ちゃんと立ち止まろう」にも繋がるが、そもそもアイデアというものは「インプットしまくって、常になんとなく考え続けて累積思考量を増やすことでなにかのきっかけでアイデアを思いつく」時間がかかる作業であるということも書いているので、即なにかが思い浮かぶと考えることが間違っている。
ちなみに、そんなことを考えていたときに以下のような記事をたまたま読んでまさに言いたいことが書いていました。しかも、「アイデアのつくり方」を引用してるという。。。
「頑張る人」はなぜ「夢中な人」に勝てないのか?つらつら考えるに、それは「累積思考量の圧倒的な違い」ということになると思います。
— 山口周 (@shu_yamaguchi) 2021年9月12日
ちゃんとモデリングができるようになろう
なんかここが課題だなー、のようなアイデアができたとしてもやり方がわからないとソリューションに結びつけることができない。
例えば、「不動産を内見して何番目の物件にしたらいいかモデルを立てたらいいのでは」ということを考えても「モデルを立てる」という行為をしたことがないとどう取り組んだらいいかわからずアイデアだけで終わる。
そもそも、「良い不動産を買おう」という課題に対してそれを数理モデルにできるということ、数理モデルにするための組み立て方を知らないと「不動産を内見して何番目の物件にしたらいいかモデル化する」という発想が出てこない。
そのため、モデリングをするという発想、どういうモデリングがあるかという慣れが必要となる*1。
具体的にどう実現するか
現状把握と定性的な解決策は出たので、具体的なアクションに落とす。
ちゃんと立ち止まろう→マインドセットを変える・即レス禁止
「何も出ない期間を恐れない」で「いったん立ち止まって考える」。そもそも「無能と思われたくないゆえに何も出ない期間を恐れる」けれど、大したものを出せないほうが無能じゃんというセルフ論駁を常にし続けて「とにかく来たものは受け入れてさっさと片付ける= 無能」として恐怖対象を変える。
これは意識の問題なので、その旨を思い出すようにslack botで仕事開始時間にリマインダーを飛ばしてマインドセットを変える。
また、何かしら判断が必要なことが来たら即レスをしない。時間をもらう。考えた上で返す。頭の中だけでそれをすると、なんとなく考えた気になりがちなので、紙などで考えをまとめたりこねくり回した上で返す。これを例外なくすべての判断が必要なことに対しておこなう。
ちゃんと楽しもう→情報への接し方を変えて楽しめる状態にする
「アイデアのつくり方」に準じて行動をする。
inputの対象に対して興味を持ってちゃんと咀嚼して面白くなるまでこねくり回す。短期間で成果が出ないのを当たり前だと感じて集めてまとめる。
「まとめる」だけだと実行可能なアクションにはなりづらいので、1日の終わりに日報のような形でslackの自分のtimes(詳細は以下記事)に書く。
また、週1か隔週かはわからないが考えた内容をビジネス系部署の人に聞いてもらう場を作ることで半強制的にやる場を作りつつ、フィードバックの場をもらう。
「アイデアのつくり方」にあるスクラップブックはmiroのデジタル付箋とかで代替。「アイデアのつくり方」と同じ発想で具体的なアクションとして書かれたKJ法は付箋を使っているため。KJ法はちゃんと学んだことがないので以下の本をさらっと読みなおす。
ちゃんとモデリングができるようになろう→モデリングという行為に慣れる
モデルのつくり方は以下の本がとても良かった。
この本であるようにちょっとした疑問をシンプルなモデルからはじめてちょっとずつ肉付けをしていく行為を繰り返していく。
繰り返していくと書いても実現可能性に乏しいので2,3日に1回その過程をnoteにアウトプットする。
ちなみに、まだ何も書いてないがこのブログではなくnoteの理由としてはただの自分用のらくがき帳なのでブログとは切り分けたいため。ある程度モデルができたらブログにまとめたい。
やっていくことの最終イメージとしては以下の記事のような内容です。
https://qiita.com/quantum-human/items/f42a298a55b917267039qiita.com
モデリングの経験ってどう積んだらいいの?という質問への解答
peing.net
あと考え方としてはこのあたりは意識すべき
楽しいことをする
ここからは仕事というよりプライベートに近い話だけれど、散々述べたように生き急ぎすぎてなんでも「処理すべき対象」としてしか見れないのが根本的な原因。要は感性が死んでる。あるいは感性に従って楽しむことへの罪悪感がある。
そういうことの連鎖や2021年色々とうまくいかないことが多すぎた結果、そもそも自分が何をしたいのかなーと考えることが多かった。正直、仕事に対してガツガツやっていくことに疲れたので何か楽しいことをしたいなーと感じていて、ちょくちょく色々なことに手を出したりしたのでその中からいくつかを本格的にやることで感性を復活させようと思う。
なお、「仕事に対してガツガツやっていくことに疲れた」と書いておきつつ仕事についてどうやったら上手くできるか的な内容を先程まで書いていたが、結局先程まで書いていたことも「仕事を楽しむとよりよく回るのでは」という話に近い。人生の時間の多くは仕事に費やすので、どうせやるなら楽しくやった方がいいし、そもそも楽しんでないから限界が見えてきたという結論が先程までの話。ここからは、仕事と完全に切り離された「楽しみ」の話。
完全に余談ですが、そういうことを考えていたときにたまたま以下の記事を読んでやっぱ楽しむ感性が死んだらだめだよな、と思いました。
コンペ参加
少し前に国内のデータサイエンスコンペのatmaCupに初参加した。
最終的にPrivate LBでもtop15%に入ってたのでまぁよしとする。やったことはGBDT系でも使えるDiscussion全部+特徴量軽く追加くらいなのでDiscussion読むの重要すね。
— チトセナガノ (@chitose_ng) 2021年10月24日
やってて色々と勉強になったのでとてもよかったです。ブログかかな。 pic.twitter.com/Kb8dsAbnbs
2週間という息切れしない期間かつ日本語だったのでとても楽しかったのでKaggleもやってみようと思う。
昔1度だけkaggle参加したときの経験から、プログラミング力とかDeep Learningできるようにならんと参加できるコンペ限られるとか諸々問題はあったが最近そのあたりをちゃんとやったので参加にあたっての問題はなくなった。
現在PetFinderコンペに参加してますが、おかげで最低限色々読んだり書いたりできるようになっており、楽しくやれているので問題なく楽しめそう(なにやったかとかはコンペ終了後に記事にする予定です)。
VR chat
数年前にVR Chatを知ってずっとやりてーなーと思っていたのですがついにOculus Quest2を買った。あとBeat SaberもしたかったのでノリでVR用にWindows PCも買った。
やってみた感想としては、VR Chatは30分くらいでVR酔いが起きる。。。VR酔いは身体感覚と視覚情報のズレが原因らしく、身体の動かし方などの慣れで改善されていくらしいので30分ずつでもいいので慣らしていく。
とりあえずは、色々知るためにVR Chatのワールドを以下のリストの上から放浪しようと思う。
あと、色々なイベントもやっているので定期的に参加する
NeosVRも面白そう
バ美肉
ノリでバ美肉用にモデルを作ってもらいました。
Vtuberデビューする気は特にないのですが、カメラで撮った自分の動きをトレースさせて動かすの楽しいんですよね。例えば前回の記事で文字説明がめんどくさかったやつは動画化しましたが楽しかった。
で、全然別の話ですが最近ボイトレを受けていてその練習として発話練習として使うのはありかなと考えてます。
ボイトレをした結果発声自体はそこそこ上達しているけれど、発話、具体的には、感情の入れ方とか抑揚とか。要するに以下の記事にあるもの。特に「アンチパターン③」にある「あー」とか「えー」とか「なんか」といったフィラー(Filler)が多い。
これの対策としては、よくプレゼンで言われているように録音して話してを繰り返すこと。ただ、何をプレゼンすんねんとか、録音聴き返しまくるモチベでねーなーとかの問題がある。
前述の記事解説動画のときは、公開する前提でやっていたので目的意識があったり、受肉してるゆえに微妙に客観的に見れたり、見ててかわいいから割と聴き返すのが苦じゃなかった。
つまり、バ美肉プレゼン練習が最高では?と思ったのでやってみる。目標がないとあれなので、いったん手持ちの過去LTしたスライドを使うと、スライドを作る労力もいらないし話す内容もある程度覚えているのでこれを練習題材として使う。
とりあえずは直近LTした以下かなぁ。それ以前のスライドはデザインが今見るとあんまり良くないけど練習だからまぁいいや。
これがある程度いけたらVtuberもどきすると楽しいのかもね。ネタないけど。
まとめ
- 「何も出ない期間を恐れない」で「いったん立ち止まって考える」、「とにかく来たものは受け入れてさっさと片付ける= 無能」というマインドセットに変えるため始業時間にslack botで通知を飛ぶようにする
- 何かしら判断が必要なことが来たら即レスせずに紙などに書いてこねくり回した上で答える。例外はない。
- 「アイデアのつくり方」に準じて情報に興味を持って接して解像度を上げるためにこねくり回しtimesに書く(平日1時間)
- 情報をまとめて出た仮説や疑問を週1で誰かにぶつける場を作る
- なにかしらのモデルを常につくり過程を定期的にnoteに吐き出す(平日朝1時間)
- Kaggleに常に参加する(平日朝1時間)
- VR chatを放浪(週1)
- バ美肉プレゼン練習(週2休憩時に30分)
基本的に「xxをやる」という目標は達成できないので、過程はnoteで書きなぐってまとまったら本ブログに書く運用。
*1:この不動産の話はグーゴルゲームというn個の数字をランダムに観察し、最大の数を当てるというモデルらしく、「秘書問題」や「お見合い問題」とも呼ばれている
CourseraのDeepLearningコース+αを使ってどうDeepLearningを勉強したか
この記事はデータラーニングギルド Advent Calendar 2021です。
この記事はなにか
データサイエンス系のMOOCとして、CourseraのMachine LearningとDeep Learningと How to Win a Data Science Competitionの3つがいいぞ、という話を目にすることが多い。
ただ、CourseraのMachine Learningコースを受けた人の記事はかなり観測できるが、DeepLearningコースを受けている人はあまり観測できなかった。英語だし結構心理的なハードルが高いと思うので興味がある人に向けて、実際受講してみて感じた知っておきたかったことなどをまとめることで興味を持った人のハードルを下げれたらと思います。

なお、このDeepLearningコースは5講座で構成されており、各講座は3,4テーマに分かれており各テーマ毎に1週(week)を想定されています。本記事では「コース」という言い回しは基本的に「DeepLearningコース」のことを指し、「講座」は「DeepLearningコースの各講座」のこと、「week」または「テーマ」は「DeepLearningコースの各講座内のあるweek(テーマ)」について指して書いています。

何を書かないか
MOOC系の記事は学んだことを自分なりに整理してまとめる、みたいな内容が多いがこの記事では講義内容についてはまとめないので興味がある人は先人である以下の記事などを参照していただけると。
特に1つ目の記事は文末に各講座の学習メモがあります。
CourseraのAndrew Ng氏によるDeep Learning Specializationを受講して - くじら公園
Python覚えて3ヶ月の素人がCoursera Deep Learning Specializationを1週間で完走した話 - Qiita
Courseraのディープラーニング専門講座を受講しました。|ドドテクノ
お前誰
データサイエンティストとして働いているものの、機械学習を使う機会はほぼなく統計モデル方面がメインです。また、機械学習もせいぜいGBDT系を使う程度のためDeep Learning系は必要としてないのでそっち方面の勉強はまったくのノー知識です(ただし、過去にCourseraのMachin Learningは修了済)。
そんな感じだったのですが、最近atmaCupに参加したのもありコンペでちゃんと遊ぶにはDeep Learningも勉強しないといけないなと感じたのでとりあえず評判が良いCourseraの本コースを受講しました。
また、データサイエンスの話題はDeep Learning系が自分の観測範囲(twitter)では多く、Deep Learning系の話題は流れてきてもなんもわからなくてもったいないからついていけるようにならんとな、というのもあります。
Pythonは稀にある機械学習系案件やコンペで使ったりでまぁ最低限は書けるかな、ってレベルです。
英語は技術記事や英論文を軽く読むくらいならまぁできるけど、細かい部分含めて理解は微妙くらいなレベルです。なお、4,5年前に受けた最後のTOEICが650点強くらいです。
数学はどうなんでしょ。もう卒業は5,6年前くらいになりますが中堅公立理系大学院卒なのでまったくないわけではないですがサボり気味だったので得意ではない自己認識です。数学系の単位落としまくってたし。
本記事の要約
- 動画なので動的に理論の理解ができるので、書籍で学ぶよりもわかりやすい
- 1日3時間を週6で1ヶ月弱の50~60時間くらいかかった
- Machine Learningコースよりプログラミング課題がやりやすかった(簡単という意味ではない)
- 日本語字幕なしは4割だが、そのうちの半分くらいはあまり英語力を必要としないしDeepLでだいたいなんとかなる
- 書籍や動画などで勉強の補完はした方がいいかも
受講してみてどうだったか
端的にいえば、細かい不満はあるもののとても良かったです。よく話題にあがる理論やその元となった理論を、図やイメージで説明しつつちゃんと数式の説明もおこなっているので結構さっくり理解が進みました。書籍による学習の場合でもそれらは載っていますが、動画ゆえに1ステップ1ステップずつ図の各場所の説明や数式への対応などを細かく丁寧におこなえるのでそこは明確に動画の強みだと感じました。
また、動画の要所要所で「○○だからXXする」みたいにちゃんとやっていることの意味も補足的にちょろっと言うみたいなことを入れやすいのも動画ならではです。
ちなみに、1テーマが終わると自分でその内容をコードで書かせるのでインプットでわかった気になるのを防ぐ効果もあります。書籍学習だとインプットしっぱなしでわかった気になった状態でその発展の次にいって、前の内容が曖昧ゆえに理解ができないみたいなことが起きがちですがそういうこともないのでインプット自体の質の向上にも繋がります。
勉強の進め方
基本的に、1week分(=1テーマ)を学んだ後に微妙によくわからない部分(自分の場合ほぼ講座4,5)があれば書籍やサイトで調べて、疑問が解決したらその週の選択形式テスト(quize)および演習をする流れで進めました。
動画の欠点でもあるのですが、書籍と違って「少し前に説明してたこれってどうだっけ?」みたいなことはしづらかったり、その前の内容を表示したまま今の内容を解釈みたいなことはしづらいのでいわゆる「立ち止まってちゃんと理解する」のは向いてないです。また、特に英語字幕のみの回はそういうことはよく起きるので何かしらの書籍は必須となります。
私が使った書籍は以下。後述しますが、この中では「ゼロから作るDeep Learning1,2」が特に理解の役に立ちました。
どれくらいの時間を使ったか
日本語字幕がある場合は1.5倍速、ない場合は1.0倍速で観ました。プログラミング課題は公式では3時間くらいかかるとありますが講座1,2,3は1時間弱くらい、講座4,5あたりは3時間くらいかかりました。
勉強時間は平日は3時間弱、土曜日は4,5時間くらい勉強をしました。
日曜日はやらなかったり、旅行で4日ほど全くやってなかったりはありましたが総計50~60時間くらいの1ヶ月弱の期間で終わらせました。公式の見積もりは週8時間で5ヶ月程度、つまり総計160時間くらいのコース設計なようですが他の方の記事を読んでいると概ね私と同じくらいなので公式の見積もりかかりすぎでは???。また、あまりよくないですがその週についてユーザーがディスカッションする場を読んだり、DeepLearningの有名人へのインタビュー動画(1時間くらい)がいくつかあったりですがそれをスキップしていたのも時間短縮の理由かも。
1week分に対して講座1,2,3あたりは3日くらいで終わらせていました(1日強で動画見る→1,2日でquizeおよびプログラミング課題を解く)。また、前述のように講座4,5では理解が曖昧な部分がちょくちょく出てきていたので講座4,5そこから+1,2日書籍などでの理解が追加されます。また、口座5はプログラミング課題が結構難しかったのでプログラミング課題は3日くらいかかっていた気がします。
英語字幕の視聴方法
右で動画を流しつつ左にDeepLで翻訳した日本語を表示して、動画に合わせてちょっとずつ手動でスクロールしています。日本語字幕ありのときは1.5倍速で観ていましたが、英語の場合は1.0倍で視聴。
ちなみに、以下の記事の方法を真似れば日本語化も可能らしい。この記事はMachine Learningコースなので、自分で字幕DL→翻訳でデータを作らないといけないので面倒ですが。自分は面倒だったのでやってないです。
【更新】Courseraのディープラーニング講座を日本語で受講する - Qiita
プログラミング課題について
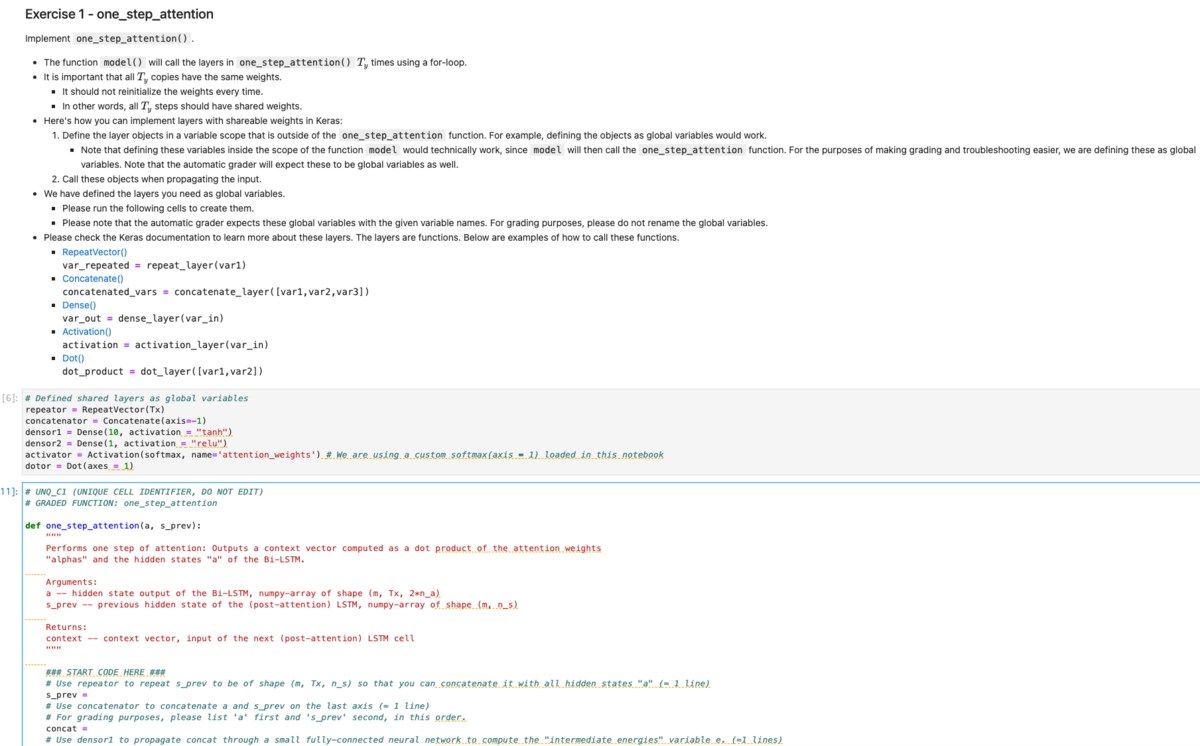
キャプチャと文字だと限界があるので、動画撮りました*1(もともとはこの記事全部口頭で解説してたのですが、45分で長すぎたのでここだけ切り抜きしました)。
このコースは全5講座×3週分前後の計14週分になっており、各週でテーマが異なります。そして各週毎にそのテーマの復習となるプログラムを提出する必要があります。
多くの人が受けているMachine Learningコースの場合は、その週で学んだ理論の実装となる問題がpdfで与えられ、Octoveという言語を用いて提出をします。
一方で、Deep Learningコースでは、その週で学んだ理論の実装となる問題がGoogle Colabolatoryのようにweb上で動作するCoursera作成*2Notebookで、Pythonを用いて提出をします。
使用する言語の違いはまぁ置いとくとして、Deep LearningコースはNotebook形式なのでプログラミング課題がMachine Learningコースと違ってかなり解きやすいです。というのも、Machine Learningではpdfの文章に小問が書かれていて、各小問に対応するpdf部分を読んで小問に対応するファイル(loopなどやデータロードなどの基本的な部分のみ実装されて学んだ箇所を書く部分は空欄)に実装コードを書いていくのですが、Deep LearningコースではNotebook内ですべてが完結しています。
つまり、Notebook内で上から順に「今回やりたいこと→小問1(実装1)でやる理論の説明→ヒント→小問1の実装コード(loopなどやデータロードなどの基本的な部分のみ実装されて学んだ箇所を書く部分は空欄)→実装が合ってるか確認する単体テスト(はじめから書かれている)→小問2でやる理論の説明→ヒント→...」という流れとなっており、実装する内容に対する理論や指示の対応関係がわかりやすくなっています。
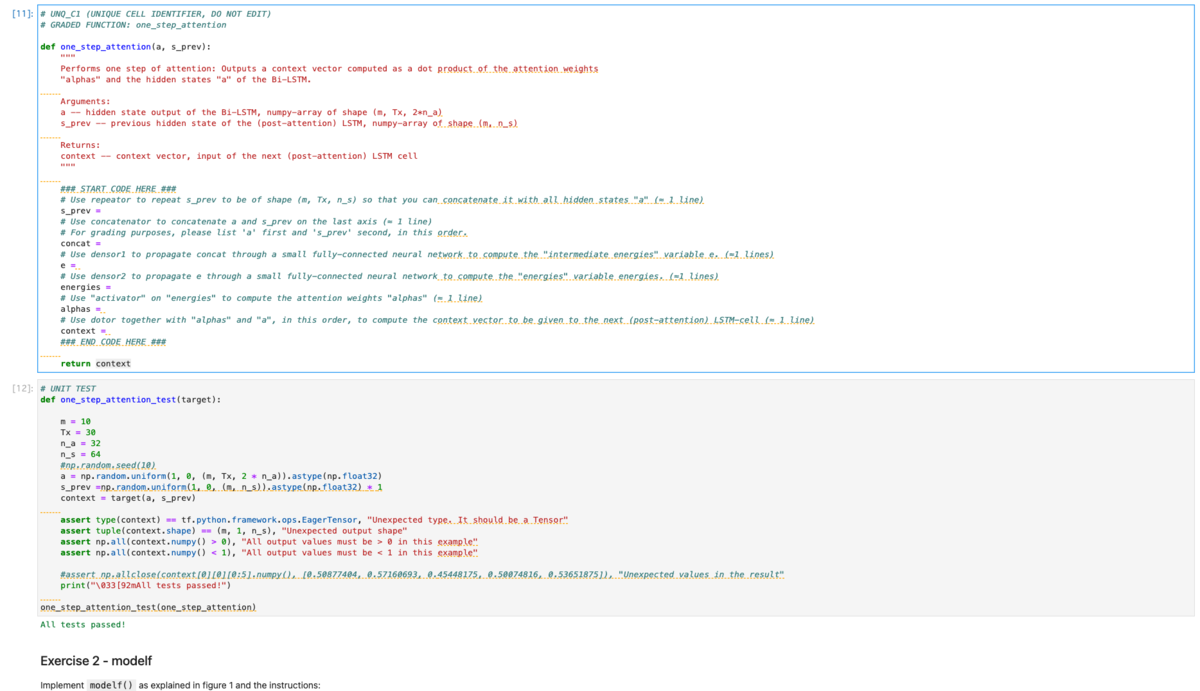
また、notebook形式なのでデバッグがやりやすいという点や、Machine Learningコースよりもヒントが充実しているという点、さらには空欄部分がMachine Learningでは「この部分に書け!(空行)」くらいだったのでほぼ0から実装だったのが、「この部分に書け!使用する変数は最低限書いておいたから=の右側を埋めろ!」くらいになっていたのでだいぶイージーになってます。なんなら「こういう順にこういうこと書いてけ」を1行毎に指示をくれる場合もあります。
Machine Learningの場合 (コードを書く場所は 「YOUR CODE HERE」部分)

Deep Learningの場合 (コードを書く場所は 「START CODE HERE 〜 END CODE HERE」部分)
日本語に関して
2021/12/7時点では以下のように大体6割が翻訳されています*3。
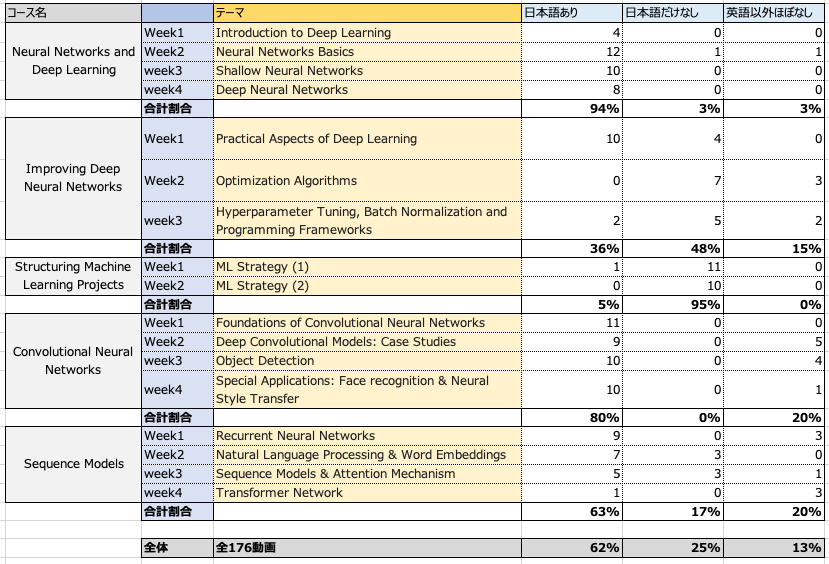
日本語がないパターンは「日本語だけなし」「英語以外ほぼなし」の2つに分けています。それぞれ、「日本語だけなし」は英語、中国語、ドイツ語、、、など多くの言語では翻訳字幕があるけど日本語だけない場合を指し、「英語以外ほぼなし」はせいぜい英語+1,2言語くらいしか翻訳されていない場合を指します。
ここをあえて分けている理由としては、やはり重要なもの複雑なものほど優先的に翻訳がされているのか「英語以外ほぼなし」の場合は翻訳優先度が低そう、つまり動画のイメージ図が豊富だったり、内容があまり複雑じゃないなどの理由で、最低限の英語レベルがあれば理解できる動画となっています。一方で「日本語だけなし」は、他の言語の多くでは翻訳されているのにも関わらず日本語だけがないので最低限の英語だと厳しい内容が多いです。
そのため、実質的にやばいのは全体を占める1割の「日本語だけなし」の動画のため、思ったより日本語の問題はない気がします。ちなみに自分の英語力は前述のように4,5年前に受けた最後のTOEICが650点強くらいです。
なお、週の最後にある選択形式のテストとプログラミング課題の小問説明はほぼDeepLに打ち込んで日本語化して読んでます。
各週の感想および日本語に関する詳細
内容に踏み込まない各週の一言感想を書きます。
また、動画ではそこそこ詳しく説明をしてくれますが、ちょっとイメージがわかりづらい部分や、理解が浅い部分があったのでそのときは別途Coursera以外のサイトや書籍を参考にしたのでその紹介もします。
それと、おまけとして前述の「日本語化」についての詳細も書きます。
Neural Networks and Deep Learning
 ニューラルネットの基本的な事項について。
ニューラルネットの基本的な事項について。
内容はMachine Learningコースのニューラルネットと同じ。時間がある分Machine Learningコースの方が丁寧かも。
Machine Learningコースでニューラルネットをちゃんと理解できていたのかサクっと終了できた。
Machine Learningコースを受講してない場合は、そもそもニューラルネットはなにをしてるかについてはアイシアちゃんの動画リスト「ディープラーニングの世界」のはじめの方(このリストはこのコースに限らず、他のコース部分もわかりやすく解説しています)、ニューラルネットのキモとなる誤差逆伝播法はヨビノリたくみさんの動画はわかりやすい。
「推定したいパラメータ数を少なくするために、パラメータ数の少ない線形結合をもとに非線形変換をしている」という説明は結構目から鱗でした。
Improving Deep Neural Networks

ディープラーニングの基本的な事項について。
ただただ深いニューラルネットを構築するだけだとこういう理由で勾配消失や学習時間がかかるーといった問題を丁寧に説明した上で、そのためのテクニックとしてAdamとかDropoutとかがどういう理屈で問題に効くか話している。
Momentum、RMSprop、Adamあたりは英語字幕だったのもあり微妙に腹落ちしきらなかったので「ゼロから作るDeep Lerning1」や各種webサイトなどをみて理解を深める。
「ゼロから作るDeep Lerning」シリーズは、コードをゼロからスクラッチで作るために理論の説明がものすごく丁寧だし翻訳本ではなく日本人が書いているのでCourseraで理解したことの復習としてめちゃくちゃわかりやすい。
ここからはTensorFlowを使用するので、TensorFlow(Keras?)を使うので基本的な使い方はこのコースを通して理解できます。また、途中で計算グラフの意味の説明もあって動画ゆえに計算の流れを丁寧に図を使って追えるのでとてもよかった。
ちなみに、この講座2から英語字幕がかなり増えつつ、次の講座3「Structuring Machine Learning Projects」もほぼ英語字幕のみなので「あ、もう日本語で理解できる部分終わったんだ。つら」って絶望しますが講座4,5は7割くらい日本語なので安心してください。
Structuring Machine Learning Projects
 機械学習プロジェクトをどう進めていくか。
機械学習プロジェクトをどう進めていくか。
例えば、testデータの精度が悪いときに考えられることとして「モデルを改善する」「データを増やす」が考えられるがどっちをやった方がいいか調査するやり方や、追加のデータが得られたときにどう考えたらいいか、など時間の制約がある中で改善効率が良い箇所をどう特定していくか。といった話。内容自体はMachine Learningコースと親しいのでサクっと理解できた。
注意点として、ここは日本語字幕はほぼなし。1つだけあるのは一番はじめのイントロ動画(数分)のみ。
ここの話は理論系ではないので、「図で理解を促す」みたいな動画の利点があまり活かせれてない(一部、表形式での説明除く)。
そのため、正直文章でも問題なさそうだったのでDeepLで全文日本語翻訳をして、文章だけでわかりづらい部分のみ該当箇所に飛んで動画をみた。つまり、ほぼ動画自体は観ないで文字で理解した。
演習課題は、実際の分析プロジェクトをもとに意思決定していくケーススタディとなっていて面白かった。
また、他の方も書いていますがこのような内容は「Deep Learning系の書籍」では学べない内容なのでとても良かったです。
Convolutional Neural Networks

CNNについて。なんで畳み込みが必要なのか、とかプーリングの意味など各レイヤーでおこなうことの意味がわかったのでDeep Learningのお気持ちが少しわかった気がする。ただ、なんでその数に畳み込むのかーみたいなのは特に説明がないがい、精度と計算時間とのトレードオフでなんとなく決めてるのかな?わからん。
ちなみに畳み込みをする理由に関して、「なんか情報を圧縮している」くらいの理解だったのですがよく考えたらよくわからんなと思ったので「畳込みがなにをやっているのか」について色々調べました。
コースの3,4週目あたりで各畳み込みが抽出している特徴を表示したりしていますが、じゃあなんでそれが畳み込みをすればわかるのか?がわかるようなわからんような、って感じでした。
このサイトの「畳み込み層」についての説明で、「特定の特徴に発火するように・・・」みたいな説明でなんとなくイメージが一段回すすみ、そのあとに実際の動きベースで「何が起きるのか」を説明している以下の動画で完全腹落ちした感じです。
なお、コース内でも同様のことは言っているので意識的に何回も考えて調べることでちゃんと理解できただけなのでそこは人によるかも。要は「なにかしらの特徴を抽出するカーネル(フィルター)を作り、それにどこが反応しているか」という観点で情報を変換し、その「なにかしらの特徴を抽出するカーネル」をいろんなバージョン作っているという意味。
また、このあたりの課題からプログラミング課題が難しくなってきたのでこのコースが用意してあるユーザーが質問をする掲示板を見るようになった。主に、詰まった関数名や小問ナンバーで検索すると、だいたい似たような質問がされているので役に立った。特に、後述する「関数の単体テストが成功していても実は関数実装が間違っているので、のちにその関数を使用した別の関数でのテストが失敗する」みたいな事象が起こりうることはここで初めて知った。
Sequence Models

RNNとその発展系について。一番最後は昨今よく聞くtransformerについてもあります。このコースは2017年くらいの授業ですが、ここまでちゃんと理解すると2021年現在よく使われている技術で何をやってるかの基本的な事項はちゃんとわかるようになっているのかな。
また、やっていること自体が文章翻訳を中心とした話でイメージがしやすいのでやっていて面白かったです。
ただし内容はそこそこ複雑になってくるので復習の必要は感じた。例えば、(日本語字幕がないということもあり)attention系(LSTM, GRU, transformer)がちょっとモヤモヤが残る理解だった。内容としてかなり重要だと思うが、基本的に字幕は「英語だけ」なのは何故なんだろう?
というわけで、ここはかなりコース外での勉強をしました。
LSTMとGRU
以下が厳密性と丁寧さのレベルがとてもバランスよくめちゃくちゃ助かった。
めっちゃ簡単に書いてるサイトも結構あるのですが、そういうのは簡略化されすぎて雰囲気しかわからん一方で、めっちゃキッチリ書いてるやつはなるほどわからんってなるからこれくらいのレベル感のサイトは本当に貴重だと思います。下記リンクは特に役に立ったLSTMとGRUのみですが、他の諸々も「用語集」から飛べます。
LSTM(Long Short-Term Memory) | CVMLエキスパートガイド
GRU(Gated Recurrent Unit) | CVMLエキスパートガイド
上記サイトで理解した後に、上記サイトと同様のレベルかつ俯瞰視点での説明をしている以下のサイトを読んで別視点から更に理解をし直した。
GRU | gated recurrent unit / RNN
また、「ゼロから作るディープラーニング2」も理論についてめちゃくちゃ丁寧だったのでこちらで理解でもよい。
また、数学部分の意味(お気持ち)はアイシアちゃんの動画がとてもよかったです。数学専攻の方だからか、「数式の意味」についてイメージをしやすいような翻訳がとても上手。
Transformer
特に、Transformerはコースの動画だけだと「何故Query, Key, Valueそれぞれがそういう役割をになったことができるか(Queryで「各単語に対してなにかしらの特徴を問い合わせる」とか)」が腹落ちしてなかったのですが、以下の動画の34分目あたりから(+後述の記事などを通した数式群の計算の流れの理解)でとても腹落ちした。
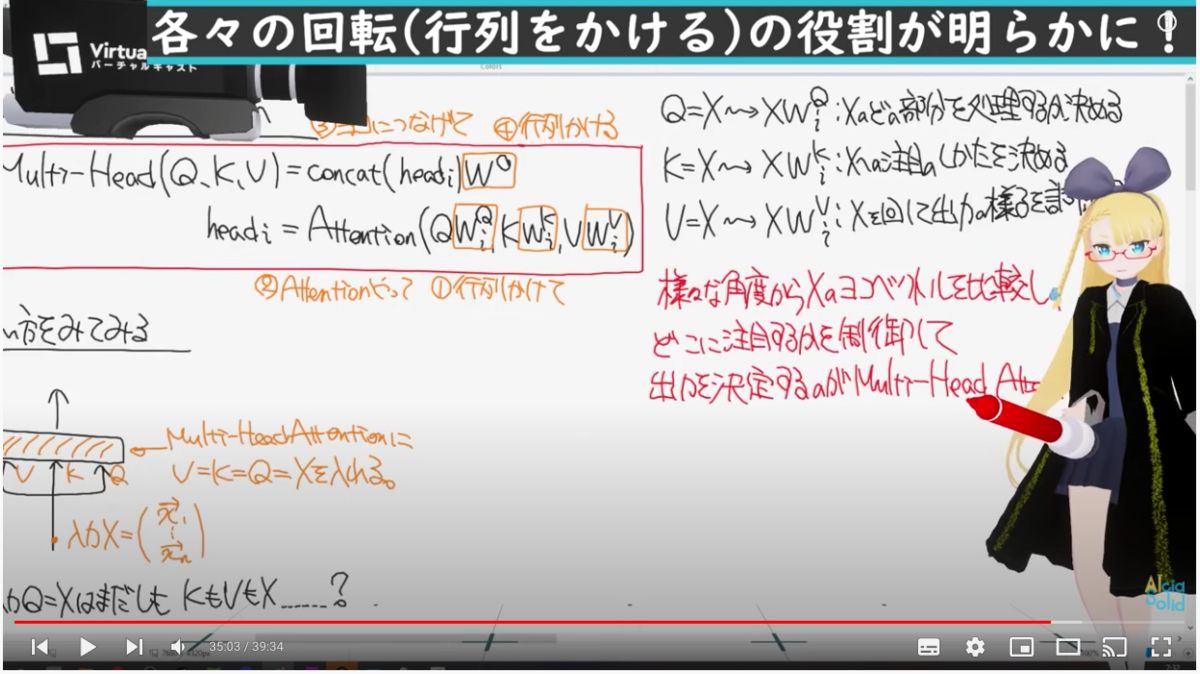
計算の流れ(=「何故Query, Key, Valueそれぞれがそういう役割をになったことができるか」)は以下の記事がとてもわかりやすかった。
Week3のプログラミング課題がかなり難しめな上に2課題あったのでちょっとつらかったですね。。。
また、Week4ではClassを作成するのですがClass作成をなれてないとコンストラクタ(__init__)やコールバック(__call__)を使用する箇所が難しそう。
ちょっと微妙だった点
全体的にとても良かったのですが、以下の点で不満を感じました。
プログラミング課題の単体テスト
プログラミング課題は、大問としてなにかの理論の実装があり、それを細かいステップの関数実装が小問としてあり最後に各関数をまとめるという流れなことが多い。その関数実装は逐一Coursera側が用意した単体テストがあるので実装が正しいかその場でわかる。・・・が、単体テストが通ってても関数群をまとめて使用する部分での結合テストで間違える場合がある。その場合は、まとめるコードが間違っているのか、関数が間違っているのかがわからないので結構時間を食うのでもうちょっとなんとかならんかなと思う。
ちなみに詰まった場合は、前述のようにCourseraが用意したユーザーの質問用掲示板があるのでそこで質問するか過去事例を探すことになる。
Jupyter LabではなくてNotebookベース
前述のように、プログラミング課題の小問毎に実装のヒントや理論の説明が書かれてからコードを書くセルがある。その説明文を参考しつつコードを書くので、コードと説明文を上下しながら読むことが多い。ただ、そのときに説明もコードセルもそこそこ長いので上下が地味に面倒。
Jupyter Labだと画面分割をしたり、段落にジャンプする機能があるがプログラミング課題は少し古めのJupyter notebookベースなのでそういうことはできない。
APIドキュメントの理解
Tensorflowのメソッドを使う際に、細かい使い方は公式APIドキュメントを見てね、という流れで挙動わかんねーなー、とかどの引数使えばいいかわかんねーなーみたいなことがちょくちょく起きた。ただ、これはメリットでもあり公式APIドキュメントを読んで使い方を知るための勉強にもなるので、つらみはあるものの避けては通れないので良い機会になった。
レイヤーの組み方の話があまりない
Poolingはロバスト性上げるとか、Convは特徴量抽出するとか、各レイヤーの単独の意味の説明はしてくれますが細かなレイヤーの話はあまりされないです。例えば、Convレイヤーを3回入れているときに2回や4回じゃなくて3回になった意味とか、何故その大きさのConvにしたのか、みたいな。
そのため良くも悪くも、プログラミング課題ではある程度指示されたステップやヒントのみでいけるので、上記のようなことは言われるがまま実装する感があったので自分で作るときに困りそうだと思いました。
実装力は自分でつける必要がある
講座5の最後あたりの課題のようにただレイヤーを足していくのではなく、loopやコールバック実装のようなことをやるのも「言われたとおりやっているだけ」なのでそこの力はつかなそう。
さいごに
不満点もちょくちょくありつつも全体的にはやってよかったなと思いました。前述のようにこのコース外での勉強もしていましたが、「動画だけでは不足している」というより私の理解力の問題な気がするのでその点は人によりけりな気がします。実際、他で学びなおしたあとに再度本コースの動画を見直すとめっちゃわかりやすかったです。ただ、「コースの動画で細かい点も含めて大まかに理解しつつ、動画だけだと理解(腹落ち)しきれなかった部分をメタ認知」→「理解しきれなかった部分を書籍などを読んだり、いろいろなサイトなどで違う角度からの説明を読んで理解をすすめる」というのは結構効率が良い勉強の流れじゃないかなと思います。
別観点の話として、「書籍のみ」の場合でも理解は進むと思いますがアウトプットによる理解のメタ認知がしづらかったり、ペースの配分は難しい気がします。また、アイシアちゃんの動画でもコース内でやっているものはほぼあるのですがこれだけだとさすがに「ざっくりポイントだけ理解」くらいになってしまいます。そのため、前述のように「Courseraコースの動画を中心として、書籍や他サイトで補完」が最適だと思いました!
おまけ
コース修了から本記事を執筆するまでの2週間強でおこなったことを書きます。
復習
記事中でも軽く載せてましたアイシアちゃんの動画はコース終了後にDeep Learning系の動画(以下リンクのプレイリスト)を全部視聴して復習やイメージの補完をした。これら動画群ではCourseraでやっていないが理解の促進や歴史的に意味があるモデルの説明や、このコース以降に出てきた有名モデル(BERTとか)の説明もしているので一通り今後もチェックしつつ観ておくとよさげ。
前述のように、数式の解釈説明がとてもわかりやすいので腹落ちしている数式に関してもとても勉強になりました。
また、改めて「ゼロからつくるディープラーニング」の1,2をさらっと読み返すました。本コースを通してだいたい理解はし終わっているのでなんとなくどうだっけ?と見返したいときなどはこの書籍があるとぱっと調べられて便利ですね。解説がめちゃくちゃ丁寧でまじで良い。今まで読んだ本の中でもトップクラス。
また、「ゼロからつくるディープラーニング3 フレームワーク編」も読みました。
ディープラーニング自体の話は1,2で終えているので、3では軽くしか書いてないです。ただ、「フレームワーク編」とあるようにKeras(tensorflow)やPyTorchのようなフレームワークをゼロからつくっていくことによって、Keras, PyTorchを使うにあたって内部的にどうなっているかがとてもわかりやすかったのでそれらを使ったコード理解がかなり進みました。
また、完全余談ですが私は自作Classを使ったコードを書く機会があまりなくたまにClassが定義されているコードを読むと理解が足りてなかったり、Classで書くと便利なんだろうなーと思うことが多々ありました。この書籍はフレームワークをつくるにあたり、Classをばりばり使っていきます。また、コードの解説がめちゃくちゃ丁寧です。そのため、この書籍をやることでClassに対して苦手意識がだいぶなくなった気がします。Python書籍としてかなり有益では。
最新論文とか有名理論とか
Courseraのこのコースは2017年末に開講されています。そのため、2021年現在でよく使われているBERTなどの説明はないです。また、この分野は発展が早く「少し前に発表されたXXXを改良したやつ作ったよー」みたいなのも多いのである程度有名どころは把握しておく必要があると思いました。
がっつりやる場合は論文とそのRefarenceを辿っていくのが良いのでしょうが、前述のアイシアちゃんの「ディープラーニングの世界」でちょくちょく新しい手法の紹介をしているので一通り視聴しました。
そのおかげでTwitterで流れてくるディープラーニングの話題や最近の手法を使った分析コードを読むときに手法XXXと書かれていても「XXXってアイシアちゃんの動画で観た!」ってなることが多かったです。
コード実装
Keras(Tensorflow)かPyTorchか、というのはDeepLearningをあまり知らない自分でもよく聞く話題なのでどちらをやるか迷いました。Kaggleなどのコンペを見ているとKeras(Tensorflow)とPyTorchは4:6くらいの比率で書かれている気がします。
色々と調べていると、どっちでもいいけどカスタマイズした細かいことやりたい場合はPyTorch、シンプルに使う分にはKerasみたいですね。
Kerasは本コースでなんとなく使い方がわかっているので、ある程度書き方が統一的フレームワークなこともありKaggleなどでコードを読んでもなんとなくわかるようになりました。一方で、PyTorchは本コースで触れないので全然わからない。6割くらいのコードが読めないのはなーということでPyTorchの本も読みました。
その中でも以下の書籍は「PyTorchの書き方を学ぶ」という観点ではかなり細かく丁寧に書かれていたのでとてもよかったですし、おかげでPyTorchのコードはなんとなく読めるようになりました。
以下の本も有名ですね。こちらは先程の書籍と比べてPyTorch自体の使い方の解説は結構さらっとしています。一方で、タイトルに「つくりながら学ぶ」とあるようにあるテーマ(物体認識とか異常検知とか)に関してどういうふうにコードを書いていくかという観点ではとてもよかったので辞書的に持っておいてもよさそう。また、前述のようにPyTorch自体の使い方はさらっとしていますが、コード全体としてはコメントが丁寧です。PyTorchはKerasと違って自分でコードを書く部分が多いのでそういう意味でも有益でした。
また、昨今自然言語処理で使われまくっているBERTくらいは軽く知っとくか・・・と思い以下の本も読みました。
レビューに書いている人もいますが、理論の説明やコード説明が結構はしょられて書いているので「なんとなくわかったけど部分的によくわからんところがある」みたいに私はなりました。そのため、疑問点を他でも学ぶ必要があるように感じました。ただ、BERTに関して書いている日本語書籍はまだ少ないのと、(自然言語処理の)辞書的な使い方としてはよさそう。
ちなみに、Keras(tensorflow)に対して書籍での理解とコンペの実コード理解のギャップを埋めるためには以下の講座が評判よいみたいです(やってないですが、必要となったらやろうと思います)。ほぼ日本語字幕があるとのこと。
おまけ2
また英語オンリーですが、スタンフォード大学のNLP+深層学習の講義がYoutubeに公開されてます。以下のは2021年度版ですが、おそらく毎年公開されるとともに毎年その段階での最新版にアップデートされていくんじゃないかなーと思います。
スタンフォード大学のNLP+深層学習の講義2021年度版が公開されていますhttps://t.co/zoGiIm6WIL
— えるエル (@ImAI_Eruel) 2021年11月7日
この講義,2年前くらいはTransformerやAttentionを講義の最終版でやってましたが,研究の加速により,この辺は当たり前と言わんばかりに中盤で消化して,後半は最近話題の言語モデル等の話になってます pic.twitter.com/Qs5VRM73pQ
また、ニューヨーク大学でも同様のものがあります。
NYU Deep Learning SP20 - YouTube
これも英語ですが、講義スライドやNotebook、講義ノート(これは日本語も!)がまとまったサイトもあります。
ニューヨーク大学のディープラーニング講義資料が公開されている。
— 🎄QDくん🎄機械学習/Python/金融工学/米国株/仮想通貨/シストレ (@developer_quant) 2021年10月22日
・講義ノートはなんと日本語にも対応
・英語だが講義スライド、Jupyter Notebook、講義動画(YouTube)も無料で見れる
・自己教師あり学習、VAEやGAN、コンピュータビジョン、自然言語処理などもカバーhttps://t.co/O2T0PDRkTs pic.twitter.com/eEiBq47xLv
atmaCup #12に参加して覚えたことメモ②lightGBM関係
これはなにか
データ分析コンペのatmaCup #12に参加して、他の人のコードを読んで覚えたことのメモです。
コンペのdiscussionで公開されているコードの書き方がとても勉強になったのですが、自分のエンジニアリング力がゴミで読解に時間がかかったので解釈用にどういう処理がされてるか読解したメモです。
コンペはよく「Discussion読もうぜ!」と聞きますが、エンジニアリング力が弱いと「そこで書かれているコードが何のコードかはコメントでなんとなくわかるけど処理がよくわからんのでただコピペしてるだけ。それを利用したり加工したりはできない・・・」となってしまうのでちゃんと書いているコードの意味も紐解きながら理解する必要があるかなぁと思います。
なお、コンペ自体はクローズドなのでポリシーに違反しないようにtitanicデータを使ってますが、一部解釈用コメントを追加したりデータに合わせて処理を加工したりしていますが元のコードコメント含めてコアとなるコードはコピペです。
また、コピペ参考元のコンペリンクは貼っているものの、コンペ参加者以外は404エラーになるのでご注意ください。そのため参考コードは引用元がわかるようTwitterリンクを貼るとともに許可を得て掲載しています。
この記事はlightGBMの処理に関して。なお、特徴量作成に関しては別記事にまとめている。
下準備
titanicを加工したデータを使う。最低限の前処理したデータをtrain testとして、それらをArrayでX,yにする
X = train.drop(['Survived'], axis=1).values y = train['Survived'].values
また、前回の記事同様に時間計測があると便利なので@nyker_gotoさん作成のTimer Classを使っている。
from time import time class Timer: def __init__(self, logger=None, format_str="{:.3f}[s]", prefix=None, suffix=None, sep=" "): if prefix: format_str = str(prefix) + sep + format_str if suffix: format_str = format_str + sep + str(suffix) self.format_str = format_str self.logger = logger self.start = None self.end = None @property def duration(self): if self.end is None: return 0 return self.end - self.start def __enter__(self): self.start = time() def __exit__(self, exc_type, exc_val, exc_tb): self.end = time() out_str = self.format_str.format(self.duration) if self.logger: self.logger.info(out_str) else: print(out_str)
Cross Validationをいい感じに実行する
Cross Validationをやるにあたり、sklearn.model_selection.cross_val_predictとかで予測値は出せるものの、各validationでのOOFの予測や学習状況、モデルや精度などを取り出すことはできない。だが、各validationで変な偏りなどが生まれていないかなどのチェックにあたってこの情報は大事。そのため、それらを取得できるように関数を作る。
内容としては、関数のパラメータとしてcross validationのFoldの取り方をlistとして渡すことで関数内部でtrainとvalidationを作成し、モデルの学習・OOFの予測・確率のラベル変換・評価をおこないモデルとOOF予測を保存・・・ということを各FoldでおこなうことでOOFの複合、つまりtrainデータに対する予測(各インスタンスはそのインスタンス学習で使われてないモデルで予測)および各Foldでのモデルを返します。また、合わせて学習時間も返します。
これは@tawatawaraさんのDiscussionを参考にさせてもらっている。
from sklearn.metrics import f1_score import lightgbm as lgbm def fit_lgbm( X, y, cv, model_params, fit_params, ): """lightGBM を Cross Validation で学習""" models = [] n_records = len(X) n_labels = len(np.unique(y)) # training data の target と同じだけのゼロ配列を用意してoofの予測値をあとで入れる oof_pred = np.zeros((n_records, n_labels), dtype=np.float32) for i, (trn_idx, val_idx) in enumerate(cv): X_trn, y_trn = X[trn_idx], y[trn_idx] X_val, y_val = X[val_idx], y[val_idx] trn_data = lgbm.Dataset(X_trn, label=y_trn) val_data = lgbm.Dataset(X_val, label=y_val) with Timer(prefix="fit fold={} ".format(i)): clf = lgbm.train( model_params, trn_data, **fit_params, valid_sets=[trn_data, val_data]) pred_i = clf.predict(X_val, num_iteration=clf.best_iteration) # binaryのpredictは1の確率のみを返すので0,1どちらともの確率となるように作り変える # 多値分類だと各ラベルの確率がpredixtが返ってくるのでこの処理は不要 pred_i_2d = [] for i, j in zip(1-pred_i, pred_i): pred_i_2d.append([i, j]) pred_i = np.array(pred_i_2d) # ======== ここまで多値分類だと不要 ======== oof_pred[val_idx] = pred_i models.append(clf) # 予測値は確率になっているので argmax でラベル化する y_pred_label = np.argmax(pred_i, axis=1) # 指標を計算する score = f1_score(y_val, y_pred_label) print(f" - fold{i + 1} - {score:.4f}") oof_label = np.argmax(oof_pred, axis=1) score = f1_score(y, oof_label, average="macro") print(f"{score:.4f}") return oof_pred, models
この関数で学習をおこなう。
Cross Validationは通常のKFoldでおこなう。
from sklearn.model_selection import KFold fold = KFold(n_splits=5) cv = fold.split(X, y) cv = list(cv) # split の返り値は generator なので list 化して何度も iterate できるようにしておく
パラメータは暫定的に以下
model_params = {
"boosting_type": "gbdt",
"objective": "binary",
"metric": "binary_logloss",
#"metric": None,
"learning_rate": 0.05,
"max_depth": 12,
"reg_lambda": 1.,
"reg_alpha": .1,
"colsample_bytree": .5,
"min_child_samples": 10,
"subsample_freq": 3,
"subsample": .8,
"random_state": 999,
"verbose": -1,
"n_jobs": 8,
# 特徴重要度計算のロジック
"importance_type": "gain",
"random_state": 71,
}
fit_params = {
"num_boost_round": 20000,
"early_stopping_rounds": 200,
"verbose_eval": 100,
"fobj": None,
"feval": None,
}
そして以下のように学習を実行
oof, models = fit_lgbm(X, y, cv, model_params, fit_params) ''' 学習過程ログ Training until validation scores don't improve for 100 rounds. Did not meet early stopping. Best iteration is: [99] valid_0's binary_logloss: 0.449694 fit fold=0 0.728[s] - fold1 - 0.7009 Training until validation scores don't improve for 100 rounds. Did not meet early stopping. Best iteration is: [53] valid_0's binary_logloss: 0.459678 fit fold=1 0.669[s] - fold2 - 0.7660 Training until validation scores don't improve for 100 rounds. Did not meet early stopping. Best iteration is: [99] valid_0's binary_logloss: 0.376929 fit fold=2 0.698[s] - fold3 - 0.8182 Training until validation scores don't improve for 100 rounds. Did not meet early stopping. Best iteration is: [100] valid_0's binary_logloss: 0.427503 fit fold=3 0.703[s] - fold4 - 0.7143 Training until validation scores don't improve for 100 rounds. Did not meet early stopping. Best iteration is: [91] valid_0's binary_logloss: 0.342852 fit fold=4 0.705[s] - fold5 - 0.8320 0.7676 '''
なお、modelsに各foldのモデルが保存されているのでモデル毎の重要度のブレつきで変数重要度をみることができる。
これは@nyker_gotoさんのdiscussionを参考にしました。
import matplotlib.pyplot as plt import seaborn as sns def visualize_importance(models, feat_train_df): """lightGBM の model 配列の feature importance を plot する CVごとのブレを boxen plot として表現します. args: models: List of lightGBM models feat_train_df: 学習時に使った DataFrame """ feature_importance_df = pd.DataFrame() for i, model in enumerate(models): _df = pd.DataFrame() _df["feature_importance"] = model.feature_importances_ _df["column"] = feat_train_df.columns _df["fold"] = i + 1 feature_importance_df = pd.concat([feature_importance_df, _df], axis=0, ignore_index=True) order = feature_importance_df.groupby("column")\ .sum()[["feature_importance"]]\ .sort_values("feature_importance", ascending=False).index[:50] fig, ax = plt.subplots(figsize=(8, max(6, len(order) * .25))) sns.boxenplot(data=feature_importance_df, x="feature_importance", y="column", order=order, ax=ax, palette="viridis", orient="h") ax.tick_params(axis="x", rotation=90) ax.set_title("Importance") ax.grid() fig.tight_layout() return fig, ax X_train = train.drop(['Survived'], axis=1) fig, ax = visualize_importance(models, X_train)
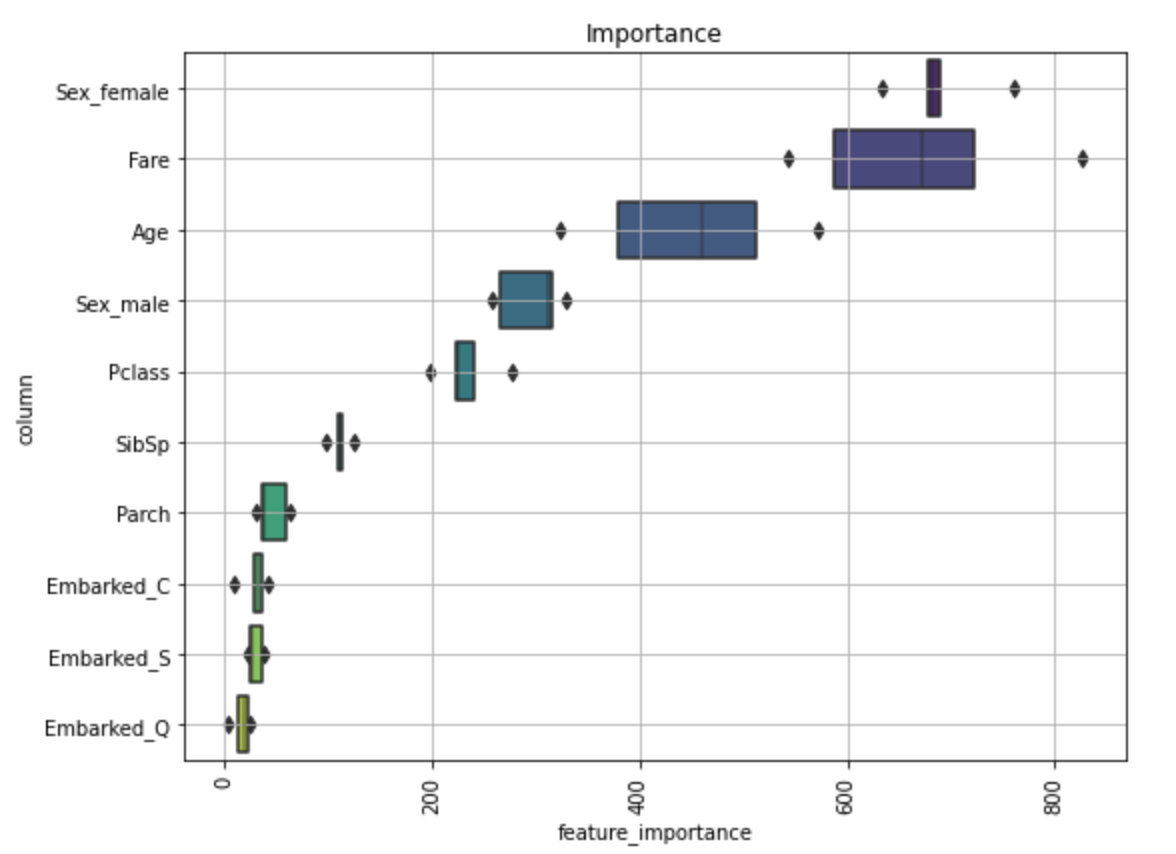
カスタムメトリクスを使う
訓練時の損失関数を自作のものにしたい場合、上記fit_lgbm関数に渡すパラメータfit_paramsのfevalに計算したい関数を指定する。また、model_paramsのmetricはNoneにしておく。理由としては何も指定しない場合はearly stoppingが、
metric になにも渡さない場合は objective (今回は binary logloss)に対応したものが metric に使用
とあるように、early stoppingが想定外の動きになることがあるため。
今回はaccuracyを損失関数にする。このcustom metricsに指定する関数は引数としてpreds(list or numpy 1-D array)、train_data(Dataset)を取り、returnとして eval_name, eval_result, is_higher_betterとなるようにする。
例えばF1-macroを使いたい場合は以下のようになる。なお、is_higher_betterはF1-macroの場合高いほどよいのでTrueにする。
def f1_macro_score(preds, data): y_true = data.get_label() y_pred = preds.reshape(len(np.unique(y_true)), -1).argmax(axis=0) score = f1_score(y_true, y_pred, average='macro') return 'macro_f1', score, True
また、今回はbinaryなので問題ないが下記の記事
注意点として、モデルが予測した値は多値分類問題であっても一次元の配列になっているため reshape する必要がある。 評価指標を計算する関数では、返り値として評価指標の名前、スコア、そしてスコアが大きい方が優れているのか否かを表す真偽値を返す。
の点は注意する。
def accuracy(preds, data): """精度 (Accuracy) を計算する関数""" y_true = data.get_label() y_pred = np.round(preds) # 0.5を閾値に変換 score = np.mean(y_true == y_pred) # name, result, is_higher_better return 'accuracy', score, True model_params = { "boosting_type": "gbdt", "objective": "binary", #"metric": "binary_logloss", "metric": None, # Noneに指定 "learning_rate": 0.05, "max_depth": 12, "reg_lambda": 1., "reg_alpha": .1, "colsample_bytree": .5, "min_child_samples": 10, "subsample_freq": 3, "subsample": .8, "random_state": 999, "verbose": -1, "n_jobs": 8, # 特徴重要度計算のロジック "importance_type": "gain", "random_state": 71, } fit_params = { "num_boost_round": 20000, "early_stopping_rounds": 200, "verbose_eval": 100, "fobj": None, "feval": accuracy, # accuracyで計算 } oof, models = fit_lgbm( X, y, cv, model_params, fit_params) ''' 学習過程ログ Training until validation scores don't improve for 200 rounds. [100] training's accuracy: 0.896067 valid_1's accuracy: 0.810056 [200] training's accuracy: 0.925562 valid_1's accuracy: 0.798883 Early stopping, best iteration is: [60] training's accuracy: 0.882022 valid_1's accuracy: 0.815642 fit fold=0 1.601[s] - fold1.8786250989595632 - 0.7886 Training until validation scores don't improve for 200 rounds. [100] training's accuracy: 0.903226 valid_1's accuracy: 0.825843 [200] training's accuracy: 0.928471 valid_1's accuracy: 0.825843 Early stopping, best iteration is: [86] training's accuracy: 0.897616 valid_1's accuracy: 0.837079 fit fold=1 1.781[s] - fold1.055654839644024 - 0.8313 Training until validation scores don't improve for 200 rounds. [100] training's accuracy: 0.896213 valid_1's accuracy: 0.865169 [200] training's accuracy: 0.920056 valid_1's accuracy: 0.859551 Early stopping, best iteration is: [77] training's accuracy: 0.889201 valid_1's accuracy: 0.876404 fit fold=2 1.694[s] - fold1.5276741576164063 - 0.8667 Training until validation scores don't improve for 200 rounds. [100] training's accuracy: 0.900421 valid_1's accuracy: 0.797753 [200] training's accuracy: 0.928471 valid_1's accuracy: 0.808989 [300] training's accuracy: 0.938289 valid_1's accuracy: 0.803371 Early stopping, best iteration is: [166] training's accuracy: 0.920056 valid_1's accuracy: 0.808989 fit fold=3 2.211[s] - fold1.943120167044094 - 0.7926 Training until validation scores don't improve for 200 rounds. [100] training's accuracy: 0.893408 valid_1's accuracy: 0.870787 [200] training's accuracy: 0.911641 valid_1's accuracy: 0.865169 Early stopping, best iteration is: [65] training's accuracy: 0.882188 valid_1's accuracy: 0.882022 fit fold=4 1.599[s] - fold1.7834760820013806 - 0.8685 0.8304 '''
atmaCup #12に参加して覚えたことメモ①特徴量作成
これはなにか
データ分析コンペのatmaCup #12に参加して、他の人のコードを読んで覚えたことのメモです。
コンペのdiscussionで公開されているコードの書き方がとても勉強になったのですが、自分のエンジニアリング力がゴミで読解に時間がかかったので解釈用にどういう処理がされてるか読解したメモです。
コンペはよく「Discussion読もうぜ!」と聞きますが、エンジニアリング力が弱いと「そこで書かれているコードが何のコードかはコメントでなんとなくわかるけど処理がよくわからんのでただコピペしてるだけ。それを利用したり加工したりはできない・・・」となってしまうのでちゃんと書いているコードの意味も紐解きながら理解する必要があるかなぁと思います。
なお、コンペ自体はクローズドなのでポリシーに違反しないようにtitanicデータを使ってますが、一部解釈用コメントを追加したりデータに合わせて処理を加工したりしていますが元のコードコメント含めてコアとなるコードはコピペです。
また、コピペ参考元のコンペリンクは貼っているものの、コンペ参加者以外は404エラーになるのでご注意ください。そのため参考コードは引用元がわかるようTwitterリンクを貼るとともに許可を得て掲載しています。
よく使う項目グループを定数化
あるデータがあって、常にgroupbyとして使うためのキーはGROUP_ID_NAME = 'id'としたり、お互い1対多結合ができるデータフレームA,BがあるときにAの特徴量をFEAT_NAMES_BASE = ['hoge','fuga','piyo']、Bの特徴量をG_FEAT_NAMES_BASE = ['address','name'] (接頭語のGはGROUPの特徴量から。つまり1対多なので結合したDFで同じGROUP(結合key)には同じ値が入る)といったように定数を置くと特徴量作成がおこないやすい。
他には、同じDF内の特徴量でも分類ができる場合それぞれ定数化すると特徴量変換がしやすい。例えばプロフィールのようなDFがあって特徴量として住所系(住んでいるところ、出身、勤務地...)、お金系(現年収、去年の年収、ボーナス...)といったものが混在している場合それぞれの定数を作成する。そうすると住所系だけ取り出したい場合はdf[住所系]のようにするといちいち住所系をすべて打ち込まなくてもよくなる。
特徴量の作成
基本的に関数化して、処理したいもとデータinputと、inputの加工結果のoutputを分けて関数の返り値とする。つまり、inputで特徴量A,B,Cがあってそれらを加工して特徴量X,Y,Zを作る場合は関数の返り値はA,B,Cを含めないX,Y,Zのみのデータとする。
要するに、関数は新たな特徴量のみが返ってくる仕様とすることで他の関数に依存しない独立した関数とすることで再現性を担保している。
例えばtitanicでNameを加工する処理は以下のようにまとめる*1。
なおデータはtitanicのtrain,teatデータをそれぞれDataFrameとしてtrain testに格納している。
def create_name_features(input_df: pd.DataFrame) -> pd.DataFrame: out_df = pd.DataFrame() # 処理自体は以下から拝借 # https://qiita.com/jun40vn/items/d8a1f71fae680589e05c # 名字 out_df['Surname'] = input_df['Name'].map(lambda name:name.split(',')[0].strip()) # Nameから敬称(Title)を抽出し、グルーピング out_df['Title'] = input_df['Name'].map(lambda x: x.split(', ')[1].split('. ')[0]) out_df['Title'].replace(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer', inplace=True) out_df['Title'].replace(['Don', 'Sir', 'the Countess', 'Lady', 'Dona'], 'Royalty', inplace=True) out_df['Title'].replace(['Mme', 'Ms'], 'Mrs', inplace=True) out_df['Title'].replace(['Mlle'], 'Miss', inplace=True) out_df['Title'].replace(['Jonkheer'], 'Master', inplace=True) return out_df create_name_features(train) # SurnameとTitleのDFが返ってくる
def create_surname_agg_feature(input_df: pd.DataFrame) -> pd.DataFrame: surname_df = create_name_features(input_df) df = pd.concat([input_df, surname_df], axis=1) surname_aggregations = [ # サンプル用なのであまり意味のない集計もしているので注意 # 平均 df.groupby('Surname')[["Age", "SibSp", "Parch"]].mean().add_prefix("mean_"), # 最小値 df.groupby('Surname')[["Age", "SibSp", "Parch"]].min().add_prefix("min_"), # 家族の数 df.groupby('Surname').size().rename("n_surname"), ] agg_df = pd.concat(surname_aggregations, axis=1) # 全結果を結合 out_df = pd.merge(df['Surname'], agg_df, on='Surname', how="left").drop(columns=['Surname']) return out_df surname_aggregations(train) # => Surnameで集計した系のDFが返ってくる
また、この関数が元データの行数を増やすような処理をおこなってないか都度テストするとロバストなので関数処理とセットでおこなうとベター
func = create_name_features for df in [train, test]: assert func(df).equals(func(df))
こちらのテスト方法は@nyker_gotoさんのdiscussionを参考にしました。
特徴量の処理の仕方
人によって何パターンかあったので2つ書く。
まとめて一気に関数処理
こちらのコードは@nyker_gotoさんのdiscussionを参考にしました。
まずは、前述のように作成した特徴量作成関数のうち、使用する関数をリストアップ
# 使用する関数
feature_functions = [
create_name_features,
create_surname_agg_feature
]
その後、引数で渡された上記関数listを1つずつ取り出し、処理をおこないつつ連結して返す関数を設定することで特徴量の処理をシンプルにおこなうことができます。
from typing import List def build_feature(input_df: pd.DataFrame, feature_functions: List) -> pd.DataFrame: # 出力するデータフレームを空で用意して out_df = pd.DataFrame() print("start build features...") # 各特徴生成関数ごとで for func in feature_functions: # 特徴量を作成し _df = func(input_df) print(f"\t- {func.__name__}:\tn={len(_df.T)}") # 横方向 (axis=1) にがっちゃんこ (concat) する out_df = pd.concat([out_df, _df], axis=1) return out_df
# 実行 feat_train_df = build_feature(input_df=train, feature_functions=feature_functions) feat_test_df = build_feature(input_df=test, feature_functions=feature_functions) X, y = feat_train_df.values, train["Survived"].values ''' start build features... - create_name_features: n=2 - create_surname_agg_feature: n=7 start build features... - create_name_features: n=2 - create_surname_agg_feature: n=7 '''
この流れのメリットは
- 関数作成パートと実際に作成するパートがはっきり分かれているため可読性が高い
- 関数listに使用したい関数を記載するだけなので、関数の取捨選択を気軽にできる
- trainとtestで漏れなく同じ関数処理ができる
一方デメリットとして、build_featureの引数がinput_dateのみであるように別の関数結果を使った処理の際に、create_surname_agg_featureのように一度別の関数を関数内では知らせる必要があり計算の無駄が発生する*2。
なお、関数処理をもうちょっと発展させてClassで処理を管理する処理の場合は過去記事の以下(作成者は同じく@nyker_gotoさん)
ひとつずつ処理
こちらは作成した関数listをもとに一気にまとめて処理するのでなく、都度処理をおこなう。
これは@tawatawaraさんのDiscussionを参考にさせてもらっている。
まずはtrain,testに関数処理をした結果の値を格納するlistおよび、作成した特徴量名を格納するlistを作成する
train_feat_list = [] test_feat_list = [] feat_names = []
次にまずはNameベースの加工をする関数を書く。これは先程と同じ処理
def create_name_features(input_df: pd.DataFrame) -> pd.DataFrame: output = pd.DataFrame() # 処理自体は以下から拝借 # https://qiita.com/jun40vn/items/d8a1f71fae680589e05c # 名字 output['Surname'] = input_df['Name'].map(lambda name:name.split(',')[0].strip()) # Nameから敬称(Title)を抽出し、グルーピング output['Title'] = input_df['Name'].map(lambda x: x.split(', ')[1].split('. ')[0]) output['Title'].replace(['Capt', 'Col', 'Major', 'Dr', 'Rev'], 'Officer', inplace=True) output['Title'].replace(['Don', 'Sir', 'the Countess', 'Lady', 'Dona'], 'Royalty', inplace=True) output['Title'].replace(['Mme', 'Ms'], 'Mrs', inplace=True) output['Title'].replace(['Mlle'], 'Miss', inplace=True) output['Title'].replace(['Jonkheer'], 'Master', inplace=True) return output
そしてこの関数処理をおこなってtrain(test)_feat_listに格納する。
# trainに対する処理 with Timer(prefix="[train] create name features:"): train_feat_list.append(create_name_features(train)) # testに対して同様の処理 with Timer(prefix="[test ] create name features:"): test_feat_list.append(create_name_features(test)) print("num of created features:", train_feat_list[-1].shape[-1]) # 直前に格納された位置=今回の処理結果を参照 feat_names.extend(train_feat_list[-1].columns) # 直前に格納された位置=今回の処理結果を参照 ''' [train] create name features: 0.008[s] [test ] create name features: 0.006[s] num of created features: 2 '''
今回Timer というものが処理に出ているがこれは処理の際に時間を測るClassとなっていて事前に実行するなりimportするなりしておく必要があります。これは詳細は割愛しますが、withで展開しつつその中に行いたい処理を書くことでその処理の時間を出力してくれるClassで便利なので合わせて使用しています。
これは先程同様@nyker_gotoさんのdiscussionコードにあるものです。
from time import time class Timer: def __init__(self, logger=None, format_str="{:.3f}[s]", prefix=None, suffix=None, sep=" "): if prefix: format_str = str(prefix) + sep + format_str if suffix: format_str = format_str + sep + str(suffix) self.format_str = format_str self.logger = logger self.start = None self.end = None @property def duration(self): if self.end is None: return 0 return self.end - self.start def __enter__(self): self.start = time() def __exit__(self, exc_type, exc_val, exc_tb): self.end = time() out_str = self.format_str.format(self.duration) if self.logger: self.logger.info(out_str) else: print(out_str)
次に、前述のcreate_surname_agg_featureと同様の結果を返すが引数で上述のcreate_name_featuresの処理結果を直接参照できるように少し変える。
def create_surname_agg_feature2(input_df: pd.DataFrame, surname_df: pd.DataFrame) -> pd.DataFrame: #surname_df = create_name_features(input_df) # 引数で参照しているので必要なし df = pd.concat([input_df, surname_df], axis=1) surname_aggregations = [ # サンプル用なのであまり意味のない集計もしているので注意 # 平均 df.groupby('Surname')[["Age", "SibSp", "Parch"]].mean().add_prefix("mean_"), # 最小値 df.groupby('Surname')[["Age", "SibSp", "Parch"]].min().add_prefix("min_"), # 家族の数 df.groupby('Surname').size().rename("n_surname"), ] agg_df = pd.concat(surname_aggregations, axis=1) # 全結果を結合 out_df = pd.merge(df['Surname'], agg_df, on='Surname', how="left").drop(columns=['Surname']) return out_df
先程の違いとしては、引数としてcreate_name_featuresの結果を渡すことで再計算を発生させてない。
また、引数に指定しているcreate_name_featuresの結果は、train_feat_listの0番目に格納されているのでtrain_feat_list[0]で取り出すことができる。
with Timer(prefix="[train] create surname_agg features:"): train_surname_df = train_feat_list[0] # create_name_featuresの結果 train_feat_list.append(create_surname_agg_feature2(train, train_surname_df)) with Timer(prefix="[test ] create surname_agg features:"): test_surname_df = test_feat_list[0] test_feat_list.append(create_surname_agg_feature2(test, test_surname_df)) print("num of created features:", train_feat_list[-1].shape[-1]) feat_names.extend(train_feat_list[-1].columns) ''' [train] create surname_agg features: 0.016[s] [test ] create surname_agg features: 0.013[s] num of created features: 7 '''
なお、この結果はtrain_feat_list[1]に格納される。
この流れのメリットは処理の再利用が可能なことがあげられる。
一方で、デメリットとしては結果を都度train_feat_listに入れているので途中で処理のミスに気づいた場合差し替えあるいはtrain_feat_listの作成時点(空list)から流し直す必要がある。また、過去の処理がtrain_feat_listの何番目にあるかが直感的に出せないのでやや面倒。ただ、そのあたりは一度作りきったら問題ないので利便性がまさる。
なお、@tawatawaraさんにお話を伺ったところ、「関数定義後その場で処理を確認したかった」とのことです。実際こちらの方が確認しながら処理をおこないやすいので好みだと思います。
また、
train_feat_listの何番目にあるかが直感的に出せないのでやや面倒
に関しては「OrderedDictとかで持ったほうがわかりやすいかも」とのこと。
実際に、単純にOrderedDictに書き換えてみると以下のような感じかなと。
# OrderedDict版 from collections import OrderedDict feat_names = [] train_feat_dict = OrderedDict() test_feat_dict = OrderedDict() with Timer(prefix="[train] create name features:"): train_feat_dict['create_name_features'] = create_name_features(train) with Timer(prefix="[test ] create name features:"): test_feat_dict['create_name_features'] = create_name_features(test) print("num of created features:", train_feat_dict['create_name_features'].shape[-1]) feat_names.extend(train_feat_dict['create_name_features'].columns) # => train_feat_dict['create_name_features']でcreate_name_featuresのDFを取り出す
ただ、この場合は関数名を何箇所も書かないといけなくてミスに繋がりそうなので、以下のように関数名を変数で格納してそれをもとに書くとよさそう
# dict版 from collections import OrderedDict feat_names = [] train_feat_dict = OrderedDict() test_feat_dict = OrderedDict() f = create_name_features # ここのみ変える f_name = f.__name__ with Timer(prefix=f"[train] {f_name}:"): train_feat_dict[f_name] = f(train) with Timer(prefix=f"[test] {f_name}:"): test_feat_dict[f_name] = f(test) print("num of created features:", train_feat_dict[f_name].shape[-1]) feat_names.extend(train_feat_dict[f_name].columns)
集約関数のエレガントな処理
前述で集約関数系をおこなったが、量が多くなると面倒なので、集約対象と集約関数のセットを渡すと集約対象名_集約関数名という列を作成するような関数を作成する。
これも@tawatawaraさんのDiscussionを参考にさせてもらっている。
import typing as tp from itertools import product def create_aggregated_feature( df : pd.DataFrame, group_ids : tp.Sequence, feature_names : tp.List[str], aggregation_names: tp.List[str], ) -> pd.DataFrame: """ pandas.core.groupby.DataFrameGroupBy.aggregate で集約特徴を作成する関数 Args: df (pd.DataFrame) : 特徴量の集約元となるデータ group_ids (Sequence) : 集約する group を示す id のシーケンス feature_names (List[str]) : 集約の対象となるカラムのリスト aggregation_names (List[str]): 集約の操作のリスト Returns: agg_feat (pd.DataFrame): 集約した特徴. index は group_id となっている. """ # # pandas.core.groupby.DataFrameGroupBy.aggregate に渡す辞書を作成 agg_dict = {} for f_name, a_name in product(feature_names, aggregation_names): agg_dict[f"{f_name}_{a_name}"] = pd.NamedAgg(column=f_name, aggfunc=a_name) # NamedAggはpandas 0.25以降 #agg_dict[f"{f_name}_{a_name}"] = (f_name, a_name) # 左記のように省略してpd.NamedAggを明示しなくても可能 # # group_id で集約. agg_dict は unpack して渡す # よくある使い方は agg(x_min=pd.NamedAgg('x', 'min'),...)だが、 # forで取り出した{f_name}_{a_name}という組み合わせ列を {f_name}_{a_name}:pd.NamedAgg(column=f_name, aggfunc=a_name) という辞書を作成し、 agg_feat = df.groupby(group_ids).agg(**agg_dict) # この辞書をaggにアンパックで渡すと、辞書のkeyが列名、valueが処理として作成できる!!!(辞書のアンパックなので複数展開される) return agg_feat
あとはこれをもとに前述の特徴量作成方法で作成
def create_surname_agg_feature3( df: pd.DataFrame, surname_df: pd.DataFrame ) -> pd.DataFrame: # Age, SibSpのmean,medianの組み合わせの4列(2*2)を作成 age_sibsp_agg = create_aggregated_feature( df, surname_df["Surname"], ["Age", "SibSp"], ["mean", "median"]) # Parchのmin,maxの2列(1*2)を作成 parch_agg = create_aggregated_feature( df, surname_df["Surname"], ["Parch"], ["min", "max"]) # # 作成した特徴量を concat. # # Surname が index なのでindex毎にくっつけてくれる all_agg = pd.concat([age_sibsp_agg, parch_agg], axis=1) # # Surnameごとの特徴量として merge agg_feat = pd.merge(surname_df[["Surname"]], all_agg, left_on="Surname", right_index=True) # # group_id を drop. mergeのときにindexがバラバラになるので元の並びに戻す agg_feat = agg_feat.drop("Surname", axis=1).sort_index() return agg_feat
実行
with Timer(prefix="[train] create surname_agg features:"): train_surname_df = train_feat_list[0] train_feat_list.append(create_surname_agg_feature3(train, train_surname_df)) with Timer(prefix="[test ] create surname_agg features:"): test_surname_df = test_feat_list[0] test_feat_list.append(create_surname_agg_feature3(test, test_surname_df)) print("num of created features:", train_feat_list[-1].shape[-1]) feat_names.extend(train_feat_list[-1].columns) ''' [train] create surname_agg features: 0.034[s] [test ] create surname_agg features: 0.022[s] num of created features: 6 '''
*1:加工自体のコードは https://qiita.com/jun40vn/items/d8a1f71fae680589e05c を参考にした
*2:少し改変したら可能ではある
順序付き多値分類を回帰問題で解くときの閾値をoptunaで求める
目的
分類クラスが順序付きカテゴリの場合、分類問題としてではなく回帰問題として解く方法がある。
その際に、例えば2.4として予測されたラベルは2とするか3とするかを判別する閾値を最適化したい。
for文を回して0.01刻みで計算して・・・という愚直なやり方でもいいが今回はoptunaを使う。
モデルはlightGBMを用い、評価指標はF1-macroとする。
データ
挙動を確認するだけなので、House Priceの住宅価格MEDVを四捨五入して10で割ったものを順序付きラベルとする(12.9ならラベル1、25.5ならラベル2となる)。
import pandas as pd import numpy as np import lightgbm as lgb import optuna import sklearn from sklearn.datasets import load_boston boston_dataset = load_boston() X = pd.DataFrame(boston_dataset["data"], columns=boston_dataset["feature_names"]) y = pd.DataFrame(np.round(boston_dataset["target"]/10,0), columns=["MEDV_per_10"]) # yを四捨五入 boston = pd.concat([X, y], axis=1) boston = boston.query("MEDV_per_10 > 0") # ラベル0は少ないので落とす # ラベル1以上でX,y作り直し X = boston[boston_dataset["feature_names"]] y = boston['MEDV_per_10'] y = y - 1.0 # 0スタートにする train_x, test_x, train_y, test_y = train_test_split(X, y, stratify=y,random_state=0)
分類問題として解く
通常通り分類問題として解くと以下のコードとなる。
def main(): num_labels = len(y.unique()) param = { 'objective': 'multiclass', 'metric': 'multi_logloss', 'num_class': len(y.unique()), 'num_leavrs': 3, 'learning_rate': 0.1 } train_xy = lgb.Dataset(train_x, train_y) val_xy = lgb.Dataset(test_x, test_y, reference=train_xy) gbm = lgb.train(param, train_xy, valid_sets = val_xy, verbose_eval=False) pred_proba = gbm.predict(test_x) pred_proba_reshape = pred_proba.reshape(num_labels, len(pred_proba)) # argmaxでlabelを取ってきやすい形にする pred_y = np.argmax(pred_proba_reshape, axis=0) # 最尤と判断したクラスを選ぶ return sklearn.metrics.f1_score(test_y, pred_y, average='macro',) print('F1:', main()) # => F1: 0.17302174216620217
F1の結果は0.17。低すぎではという疑問はありつついったん次にいく。
回帰問題として解く
連続値の予測部分
いったん回帰モデルで予測した部分のみ抜粋する。
param = {
'objective': 'regression',
'boosting_type': 'gbdt',
'num_leavrs': 3,
'learning_rate': 0.1
}
train_xy = lgb.Dataset(train_x, train_y)
val_xy = lgb.Dataset(test_x, test_y, reference=train_xy)
gbm = lgb.train(param,
train_xy,
valid_sets = val_xy,
verbose_eval=False)
# testの予測(連続値)
pred_cont_y = gbm.predict(test_x)
パターン1.Clipping+四捨五入でラベル化する
いったん、閾値をもとに予測された連続値をラベルに変換するのではなく単純にClipping+四捨五入でラベル変換をおこなう
pred_label_y = np.clip(pred_cont_y, min(y), max(y)).round() # clip+round f1 = sklearn.metrics.f1_score(test_y, pred_label_y, average='macro',) print('F1:', f1) # => F1: 0.6679785299898898
このとき、F1: 0.6679785299898898となる。
パターン2. Optunaで閾値を探索してラベル化する
本題。OptunaでF1最大となる閾値を探索する。
なお、基本的な使い方は過去記事に書いた
今回はラベルは0~4の5種類ある。そのため、0と1の閾値、1と2の閾値...といったように閾値を4つ作成する必要がある。
計算時に変数を用いる
今回は連続予測値yをラベル予測値yに変換(ここを上手く最適化したい)した値をy実測値と照らしあわせてF1を計算し、これを最適化する。そのため、Optunaの目的関数としてこの連続予測値y、y実測値変数が必要となる。
しかし、Optunaの目的関数には以下の記事
Optunaは
study.optimizeは関数オブジェクトを受け取っている。言い換えると objective は trial : optuna.Trial というただひとつの引数だけを受付ける関数であるという前提がある。
とあるように、trial : optuna.Trial以外の引数は受付けないため計算に変数を渡すことができない。
対応策1.高階関数
この対応としては1つは上記記事のように高階関数として記載する方法がある。
import warnings def objective(true_y, pred_cont_y): def _objective(trial): # 引数 (trial) はTrial型の値 warnings.simplefilter('ignore', category=RuntimeWarning) # RuntimeWarningを無視扱いに設定 num_labels = len(true_y.unique()) labels = np.unique(true_y) thresholds = [] for i in range(num_labels - 1): # 閾値数=label-1 # 探索範囲: i=0ではラベル最小(0) ~ ラベル最大、それ以外ではi-1の閾値 ~ ラベル最大 low = max(thresholds) if i > 0 else min(labels) # 下限:i-1の閾値最小(i=0のときはラベルの下限) high = max(labels) # 上限:ラベル最大 # 閾値の最適候補を探索し、追加する t = trial.suggest_uniform(f't{i}', low, high) thresholds.append(t) pred_label_y = pd.cut(pred_cont_y, [-np.inf] + thresholds + [np.inf], # [-inf, thresholds, inf]で区切られる labels=labels # 区切りに対してラベルを対応させる ) return sklearn.metrics.f1_score(test_y, pred_label_y, average='macro',) return _objective
この書き方でもいいが、functools.partialを用いて以下のように表現する方法もある。
def tmp_objective(true_y, pred_cont_y, trial):# 引数 (trial) はTrial型の値 warnings.simplefilter('ignore', category=RuntimeWarning) # RuntimeWarningを無視扱いに設定 num_labels = len(true_y.unique()) labels = np.unique(true_y) thresholds = [] for i in range(num_labels - 1): # 閾値数=label-1 # 探索範囲: i=0ではラベル最小(0) ~ ラベル最大、それ以外ではi-1の閾値 ~ ラベル最大 low = max(thresholds) if i > 0 else min(labels) # 下限:i-1の閾値最小(i=0のときはラベルの下限) high = max(labels) # 上限:ラベル最大 # 閾値の最適候補を探索し、追加する t = trial.suggest_uniform(f't{i}', low, high) thresholds.append(t) pred_label_y = pd.cut(pred_cont_y, [-np.inf] + thresholds + [np.inf], # [-inf, thresholds, inf]で区切られる labels=labels # 区切りに対してラベルを対応させる ) return sklearn.metrics.f1_score(test_y, pred_label_y, average='macro',) objective = partial(tmp_objective, test_y, pred_cont_y)
対応策2. Objective Class+call
他の対応としては、Classを作成し、__call__で最適化したい計算を返すようにすることでstudy.optimize時にこのClassのインスタンスを関数のように用いることができる。
そして、インスタンス変数として使用したい引数を渡す仕様にすると結果的に計算に変数を渡すことができる。
class OptunaRounder: def __init__(self, true_y, pred_cont_y): self.true_y = true_y self.pred_cont_y = pred_cont_y self.labels = np.unique(true_y) self.num_labels = len(self.labels) def __call__(self, trial): """最大化したい目的関数""" thresholds = [] for i in range(self.num_labels - 1): # 閾値数=label-1 # 探索範囲: i=0ではラベル最小(0) ~ ラベル最大、それ以外ではi-1の閾値 ~ ラベル最大 low = max(thresholds) if i > 0 else min(self.labels) # 下限:i-1の閾値最小(i=0のときはラベルの下限) high = max(self.labels) # 上限:ラベル最大 # 閾値の最適候補を探索し、追加する t = trial.suggest_uniform(f't{i}', low, high) thresholds.append(t) pred_label_y = pd.cut(self.pred_cont_y, [-np.inf] + thresholds + [np.inf], # [-inf, thresholds, inf]で区切られる labels=self.labels # 区切りに対してラベルを対応させる ) return sklearn.metrics.f1_score(self.true_y, pred_label_y, average='macro',) objective = OptunaRounder(test_y, pred_cont_y)
[参考]
最適化の実行
前述のなにかしらの方法で、閾値をもとにラベル変換してF1計算の結果が返ってくるobjective関数(インスタンス)を作成し最適化をおこなう。
study = optuna.create_study(direction="maximize") # 最適化処理を管理するstudyオブジェクト study.optimize(objective, # 目的関数 n_trials=30, # トライアル数 timeout=60 ) print(study.best_value) # => 0.7358186890336309
F1は0.7358186890336309でClipping+四捨五入の0.6679785299898898より改善している。
なお、今回はtrialは30としているがもっと回すとより高い値になる可能性もある(ちなみに、ときどきtrial途中で詰まって終わらないことがあり、timeout設定をしても強制終了してくれないことがあってよくわからん。。。)
ちなみにこのときの閾値は以下
print(study.best_params)
{'t0': 0.6448355141969913,
't1': 1.6126196134062987,
't2': 2.67914828011351,
't3': 2.9543708468573566}
pipeを用いてpythonを極力メソッドチェーンで書く
この記事はなにか
可読性/保守性を上げるために、できる限りメソッドチェーンで書きたい。
過去にメソッドチェーンについての記事は書いたが、どうしてもメソッドチェーンで完結できない処理もあるのでめんどくさいなーと思っていた。
最近以下の記事を読んで、 「どうしてもメソッドチェーンで完結できない処理」もpipe + 関数化で処理できそうなのでメモがてらに試してみる。
なお、そもそも関数化することでテストすることができたり、使い回しが容易になるなどの副次効果もある。
言われてみたらメソッドチェーンで完結できない処理も関数化してpipeでうまいことできるのは当たり前だが、地味に盲点でした。
以下、上記事のコードをベースに記載をする。
使用データはtitanic
やりたいこと
- Nameを姓名に分けたい
- Sex列のmaleをM、femaleをFに変換したい
- 年齢不明の場合、何かしらの数値に置き換えたい(同Pclassの平均値にしたい)
- 年齢に応じたグループ age ranges: ≤12, Teen (≤18), Adult (≤60), and Older (>60) を作成したい
これらをpipeを使わない場合と使う場合で比較したい
pipeを使わないで処理をする
pipeを使わないで普通に書くと以下のようになる。
# 0. data load df = pd.read_csv('./data/titanic/train.csv') # 1. Nameを姓名に分けたい def split_name_series(string): # 2列要素を作成して返ってくるのでindexを付けたSeriesとして返す firstName, secondName=string.split(', ') return pd.Series( (firstName, secondName), index='firstName secondName'.split() ) # Select the Name column and apply a function name_split=df['Name'].apply(split_name_series) df=pd.concat([df,name_split],axis=0) # 2. Sex列のmaleをM、femaleをFに変換したい mapping={'male':'M','female':'F'} df['Sex']=df['Sex'].map(mapping) # 3. 年齢不明の場合、何かしらの数値に置き換えたい(同Pclassの平均値にしたい) pclass_age_map = { 1: 37, 2: 29, 3: 24, } cond=df['Age'].isna() res=df.loc[cond,'Pclass'].map(pclass_age_map) df.loc[cond,'Age']=res # 4. 年齢に応じたグループ age ranges: ≤12, Teen (≤18), Adult (≤60), and Older (>60) を作成したい bins=[0, 13, 19, 61, sys.maxsize] labels=['<12', 'Teen', 'Adult', 'Older'] ageGroup=pd.cut(df['Age'], bins=bins, labels=labels) df['ageGroup']=ageGroup
セルごとに処理を分けると以下のようなキャプチャになる。

このような書き方の場合以下のような問題がある
dfが上から順に流さないといけない(今回はどの順番でもいいが)df自体に対しての処理がどこかわかりづらい- 一部処理をやめたいときにコメントアウトの範囲が広くて見づらい
- テストがしづらい
なお、1.は各処理で格納する変数名を変えると解決はできるがその場合無駄にオブジェクトをいっぱい作成することになる。
pipeを使って処理
pipeを使う場合以下のようにまず処理を関数化する。
# 0.data load def load_data(): return pd.read_csv('./data/titanic/train.csv') # 1. Nameを姓名に分けたい def split_name(x_df): def split_name_series(string): firstName, secondName=string.split(', ') return pd.Series( (firstName, secondName), index='firstName secondName'.split() ) # Select the Name column and apply a function res=x_df['Name'].apply(split_name_series) x_df[res.columns]=res return x_df # 2. Sex列のmaleをM、femaleをFに変換したい def substitute_sex(x_df): mapping={'male':'M','female':'F'} x_df['Sex']=x_df['Sex'].map(mapping) return x_df # 3. 年齢不明の場合、何かしらの数値に置き換えたい(同Pclassの平均値にしたい) def replace_age_na(x_df, fill_map): cond=x_df['Age'].isna() res=x_df.loc[cond,'Pclass'].map(fill_map) x_df.loc[cond,'Age']=res return x_df # 4. 年齢に応じたグループ age ranges: ≤12, Teen (≤18), Adult (≤60), and Older (>60) を作成したい def create_age_group(x_df): bins=[0, 13, 19, 61, sys.maxsize] labels=['<12', 'Teen', 'Adult', 'Older'] ageGroup=pd.cut(x_df['Age'], bins=bins, labels=labels) x_df['ageGroup']=ageGroup return x_df
その後、pipeで処理をおこなう。
# pclass毎での平均年齢 pclass_age_map = { 1: 37, 2: 29, 3: 24, } res=( load_data() .pipe(split_name) .pipe(substitute_sex) .pipe(replace_age_na, pclass_age_map) .pipe(create_age_group) ) res.head()

このとき、
1. 関数で処理が分けられているので何をしているのかわかりやすい
2. 処理が関数で切り分けられているので、testなどがおこないやすい。また、再利用が可能になる。
3. pipeを用いずに過去記事のようにpandasの規定関数そのものを繋げていく場合と比べて可読性が高い
4. 関数+pipeの場合、pd.concatやpd.mergeのようにメソッドチェーンで繋げない処理をpipeを使うとメソッドチェーンの流れに落とし込むことができる
5. 関数+pipeの場合、上記自作関数substitute_sexのように処理に使う引数の定義を関数に内包できる。関数化をしない場合はメソッドチェーンの外にまとめておくのでどの処理で使っているかわからないし、そもそもpandasメソッドのみでつないだメソッドチェーンの引数で渡さないといけなくて面倒。
6. pandasメソッドのみでのメソッドチェーンに合わせた書き方をしないでよくなる。例えば、列追加のときにメソッドチェーンだとassignを使ってめんどくさい書き方になるが関数内で df['X] = xxxのようにシンプルに書くことができるとか、上記自作関数split_nameのようにSeriesで処理を書けるなど
といったメリットがあり、総じて可読性、頑強性の意味で使いやすい。
余談
メソッドチェーンや、dplyrのパイプ演算子(%>%)は関数型プログラミング的な概念なのかなー。
jupyterで初心者が書きがちなのは手続き型。
Jupyter noebookでデバッグをする方法
この記事はなにか
以下のTweetを見て知らなかったので、自分で手を動かした
まじでマジックコマンドの"%debug"便利なのでjupyter使ってる人で知らない人いたら一度使ってみてほしい。。。
— fkubota🦉 (@fkubota_) 2021年7月27日
「知らんかった!!」っていう人があまりにも多い。。。
わざわざgif作ったよ!
「エラー出た!!」で後出しでデバッグできるんだから使わない手はないよね。 pic.twitter.com/t2yjMqn1vV
なお、Tweet元の方がその後LTをした資料は以下。
pdb/ipdb と jupyterのマジックコマンド %debug それぞれの説明をしている。
サンプル用notebookコードもある。基本的にこのcolabを動かしたらすべてわかる感はある。
なお、
僕は以下のような使い分けをしています。 pdb/ipdb: 誰かが書いた クラス とか 関数 の深いところを動かしながら確認したいとき。 %debug: エラー出た。。。なぜ。。。のとき。 状況にも寄りますが大体こんな感じです。 printデバッグも頻繁にやりますが、あきらかにデバッガを使ったほうが楽なシーンもあるので使い分けてください。
とのこと。
本記事は実際に動かした感想および自分用のメモとしてコマンドなどを残す意図です。
ドキュメントはpdbのデバッガコマンド部分がpdb および %debugで使える。
以下の記事でもよい
debug対象
以下の記事で作った外れ値の書き換えコードを動かして挙動を確認する。
class FeatureClipper(BaseEstimator, TransformerMixin): def __init__(self, cols_to_clip_lower=None, cols_to_clip_upper=None): self.cols_to_clip_lower = cols_to_clip_lower self.cols_to_clip_upper = cols_to_clip_upper def fit(self, X, y=None): # 各特徴量の0.001, 0.999パーセンタイル点を取得 self.lower_bounds = {c: X[c].quantile(0.001) for c in self.cols_to_clip_lower} self.upper_bounds = {c: X[c].quantile(0.999) for c in self.cols_to_clip_upper} return self def transform(self, X): # 直接の書き換えが起きないようにcopy _X = X.copy() # 各特徴量を0.999パーセンタイル点に収める(0.999を超える値は0.999で置き換え) if self.cols_to_clip_lower is not None: for c in self.cols_to_clip_lower: _X[c] = _X[c].clip(lower=self.lower_bounds[c]) # 各特徴量を0.001パーセンタイル点に収める(0.001より小さい値は0.001で置き換え) if self.cols_to_clip_upper is not None: for c in self.cols_to_clip_upper: _X[c] = _X[c].clip(upper=self.upper_bounds[c]) return _X
元記事同様、このTransformerを使ってClip処理をfit_tranformを用いておこなう。
まずはClip処理をわかりやすくするために、boston住宅価格データに加工をおこなう。
#ボストン住宅価格データセットの読み込み from sklearn.datasets import load_boston boston = load_boston() #説明変数 X = pd.DataFrame(boston.data, columns=boston.feature_names) # CRIM列をテキトーに外れ値に置き換える X.iloc[0,0] = -500 X.iloc[1,0] = 500
%debugでエラーが起きた原因を調べる
次に、以下のようにtranceformerを適用する。
# Transformerの適用 # 各特徴量を0.999, 0.001パーセンタイル点に収める(超える値は0.999,0.001で置き換え) tranceformer = FeatureClipper() X_clipped = tranceformer.fit_transform(X)
エラーが出るので%debugを起動。
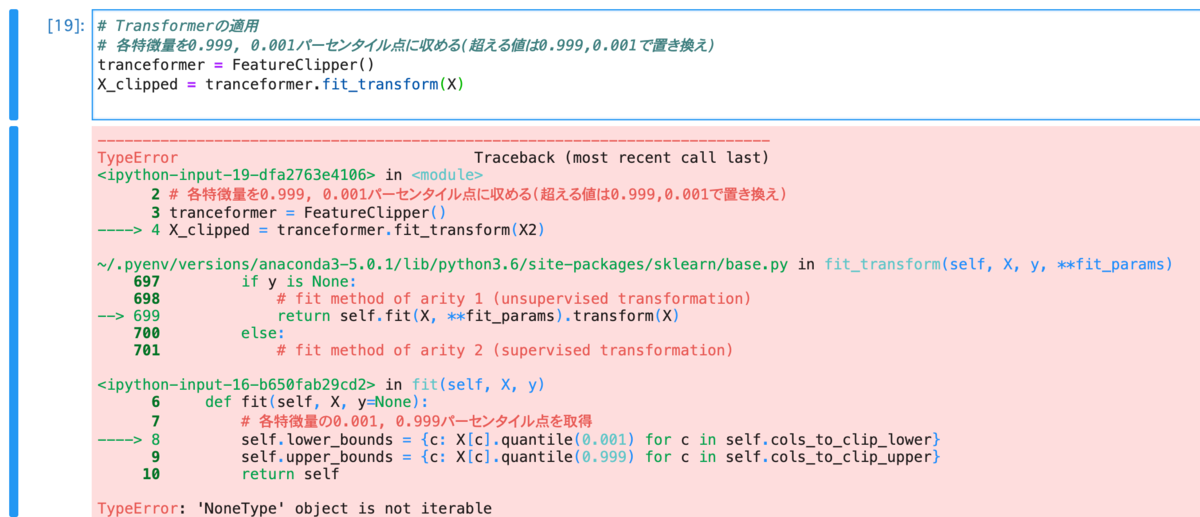
lでエラー箇所の前後5行を見ると、fit 関数の self.lower_bounds = {c: X[c].quantile(0.001) for c in self.cols_to_clip_lower}がエラー。内容としては、 TypeError: 'NoneType' object is not iterable。
u で上のフレーム(深さ)までいくと、 fitの適用時のエラー、更にuで上にいくとfit_transformを使ったときのエラーということがわかる。

ちなみに、 llで現在の関数またはフレーム全体を表示したり、l 12 のように引数指定で前後5行を見る中心行を指定することができる。
まぁこのあたりは正直エラー文自体で見れるけど今回はフレームや、記載量が少なかったのでもうちょっと複雑なコードだと必要になりそう。
dを2回押してはじめのフレームに戻る。
self.lower_bounds = {c: X[c].quantile(0.001) for c in self.cols_to_clip_lower} がエラーのようなので、いったん変数cを見るためにpコマンドを使う。
ipdb> p c *** NameError: name 'c' is not defined
「cが定義されてない」と出る*1のでcのもととなるself.cols_to_clip_lowerを見る。
ipdb> p self.cols_to_clip_lower None
self.cols_to_clip_lower はNoneとしてこのコードが走っていることがわかる。つまり、self.cols_to_clip_lower がNoneなのでcが定義されず、そのためX[c].quantile(0.001)のX[c]を定義することができずエラーが発生していたことになる。
では、そもそも何故self.cols_to_clip_lower はNoneだったのかを考えると、以下のようにclass定義時の初期値がcols_to_clip_lower=Noneとして設定されている。
class FeatureClipper(BaseEstimator, TransformerMixin): def __init__(self, cols_to_clip_lower=None, cols_to_clip_upper=None): self.cols_to_clip_lower = cols_to_clip_lower self.cols_to_clip_upper = cols_to_clip_upper (略)
そのため、tranceformerインスタンスを定義しているときtranceformer = FeatureClipper()に引数で初期値を渡していないのでデフォルトのNoneとして作成されることとなっている。
# Transformerの適用 # 各特徴量を0.999, 0.001パーセンタイル点に収める(超える値は0.999,0.001で置き換え) tranceformer = FeatureClipper() X_clipped = tranceformer.fit_transform(X)
そのため、以下のように引数としてClipをおこないたい列をlistで渡してインスタンスを作成する。
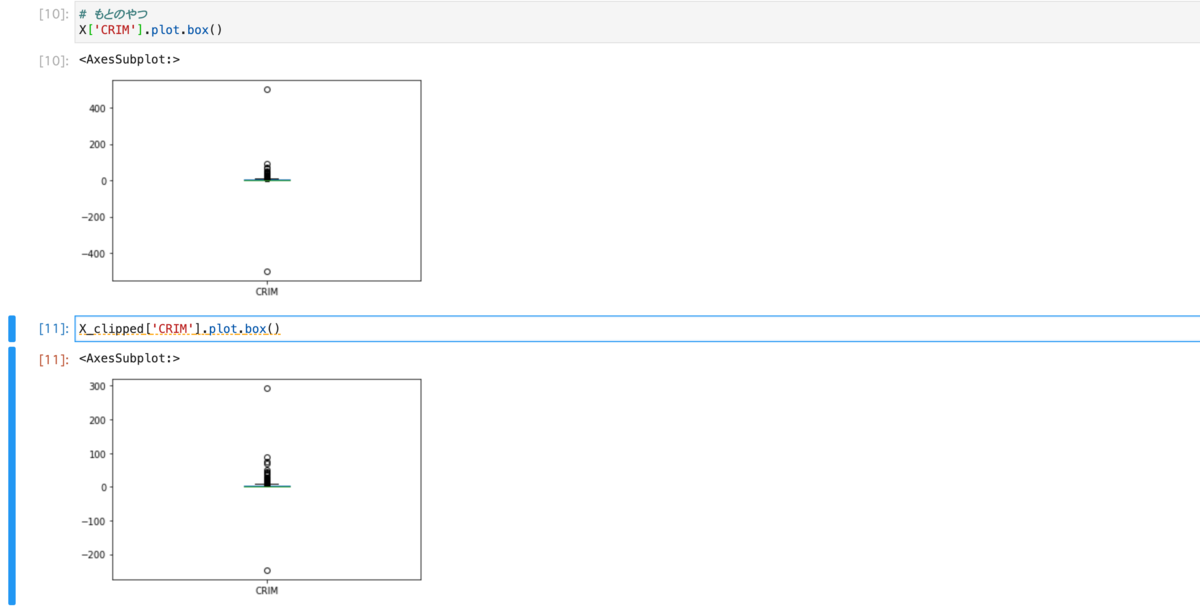
# Transformerの適用 # 各特徴量を0.999, 0.001パーセンタイル点に収める(超える値は0.999,0.001で置き換え) tranceformer = FeatureClipper(cols_to_clip_lower=['CRIM', 'ZN'], cols_to_clip_upper=['CRIM','ZN']) X_clipped = tranceformer.fit_transform(X)
そうするとエラーが起きない。
また、結果を見るとちゃんとClipが機能していることもわかる。
定義したClassの挙動を確認する
次は実際にtranceformer.fit_transform()をおこなったときに、内部でどのような挙動が起きているか確認する。これは、自分でclassなり関数なりを定義したときに思っていた挙動と違う場合に役に立つ。
やり方としては、チェックしたいタイミングの行にst()を置くとそのタイミングで内部の状態がどうなっているか調べることができる。
なお、前節の%debugはデフォルトで入っているが、st()はpdbからset_traceをimportする必要があるので事前にfrom pdb import set_trace as stと宣言しておく。
今回はClipされる各特徴量の0.001, 0.999パーセンタイル点がいくらか調べるために、fitの最終行にst()を仕込む。
class FeatureClipper(BaseEstimator, TransformerMixin): def __init__(self, cols_to_clip_lower=None, cols_to_clip_upper=None): self.cols_to_clip_lower = cols_to_clip_lower self.cols_to_clip_upper = cols_to_clip_upper def fit(self, X, y=None): # 各特徴量の0.001, 0.999パーセンタイル点を取得 self.lower_bounds = {c: X[c].quantile(0.001) for c in self.cols_to_clip_lower} self.upper_bounds = {c: X[c].quantile(0.999) for c in self.cols_to_clip_upper} st() # <= ****************** この部分でチェックしたい ****************** return self def transform(self, X): # 直接の書き換えが起きないようにcopy _X = X.copy() # 各特徴量を0.999パーセンタイル点に収める(0.999を超える値は0.999で置き換え) if self.cols_to_clip_lower is not None: for c in self.cols_to_clip_lower: _X[c] = _X[c].clip(lower=self.lower_bounds[c]) # 各特徴量を0.001パーセンタイル点に収める(0.001より小さい値は0.001で置き換え) if self.cols_to_clip_upper is not None: for c in self.cols_to_clip_upper: _X[c] = _X[c].clip(upper=self.upper_bounds[c]) return _X
%debug同様に、p 変数でそのタイミングでの変数の状態を出力できるので、0.001パーセンタイル点self.lower_boundsと0.999パーセンタイル点self.upper_boundsを見る。

すると、CRIM, ZNそれぞれの0.999,0.001パーセンタイル点の値を確認することができる。
これはつまり、transform時にclip関数の引数として渡される値なのでこれらの値以上/未満はこの値に置換されることを意味する。
また、よくある使い方としては冒頭に記述した参照元スライドにあるサンプルコードのようにforループ内にst()を起き、b (行数)でブレークポイントを設定しつつnやcでループを進めることでループ毎での変数の変化を確認するなどがある。
*1:書き終わってから気づきましたが、よく考えたら辞書内包表記なのでエラー出てなくても外側からみてcは定義されてない。cも調べたい場合は辞書内包表記ではなくて、for文とかで書く













